Podstawy analizy danych

Numpy
Matplotlib
Pandas
Math & Scipy
~~OpenCV~~
~~Tensorflow & Scikit-learn~~

Cover photo by Markus Spiske on Unsplash

1. Numpy

Podstawowe informacje
Ndarray
Podstawowe operacje na tablicach wielowymiarowych
Algebra liniowa

1. Podstawowe informacje

NumPy to skrót od Numerical Python, jest to podstawowa biblioteka do obliczeń liczbowych w Pythonie. Większość bibliotek zorientowanych naukowo silnie współpracuje z obiektami tablicowymi Numpy dlatego opanowanie podstaw tej biblioteki jest esencjonalnie związane z dalszą podróżą w analizę danych. Częściowo napisana w C/C++ umożliwia szybkie operacje na danych. Operacje pakietu Numpy mogą w złożony sposób przetwarzać całe tablice bez wykorzystywania pętli.

Przydatne linki:

https://numpy.org
https://numpy.org/doc/1.17/user/quickstart.html
https://docs.scipy.org/doc/numpy/user/index.html
https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.html
https://towardsdatascience.com/the-easiest-python-numpy-tutorial-ever-5c206c809a0d

Porównanie wydajności:

import numpy as np
numpy_array = np.arange(1000000)
python_list = list(range(1000000))

%time for _ in range(10): npa_2 = numpy_array * 2

CPU times: user 13 ms, sys: 4 ms, total: 17 ms
Wall time: 21.3 ms

%time for _ in range(10): pl_2 = [x * 2 for x in python_list]

CPU times: user 612 ms, sys: 160 ms, total: 773 ms
Wall time: 776 ms

2. Ndarray

Ndarray - n d immensional array (pol. tablica n-wymiarowa)

Jest podstawowym obiektem biblioteki Numpy. Jest to kontener przeznaczony do przechowywania dużych zbiorów danych.

Syntax:

class numpy.ndarray(shape, dtype, ...)

shape - wymiary utworzonej tablicy

dtype - typ danych przechowywanych w tablicy (cała tablica przechowuje tylko jeden)

Tablice n-wymiarowe można tworzyć z wcześniej utworzonych list lub krotek pythonowych przy pomocy polecenia

np.array()

Przykład:

import numpy as np

lista = [1, 2, 3, 4]
nd_arr = np.array(lista)
print(nd_arr)
print(type(nd_arr)) # typ 
print(nd_arr.shape) # wymiary
print(nd_arr.dtype) # typ danych przechowywanych

[1 2 3 4]
<class 'numpy.ndarray'>
(4,)
int64

nd_arr_2 = np.ndarray(lista)
print(nd_arr_2)
print(type(nd_arr_2)) # typ 
print(nd_arr_2.shape) # wymiary
print(nd_arr_2.dtype) # typ danych przechowywanych

[[[[1.601345e-316 5.075659e-317 7.213358e-322           nan]
   [0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000]
   [0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000]]

  [[0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000]
   [0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000]
   [0.000000e+000 0.000000e+000 0.000000e+000 0.000000e+000]]]]
<class 'numpy.ndarray'>
(1, 2, 3, 4)
float64

Zwróćmy uwagę na wymiary (1, 2, 3, 4)

1 klamra zawierająca 2 klamry,
zawierajace 3 klamry,
zawierajace 4 wartości losowe.

Nasz parametr listy został zinterpretowany jako shape !!!

nd_arr_3 = np.ndarray(shape=(4,1), dtype=int)
print(nd_arr_3)
print(type(nd_arr_3)) # typ 
print(nd_arr_3.shape) # wymiary
print(nd_arr_3.dtype) # typ danych przechowywanych

[[4607182418800017408]
 [4607182418800017408]
 [4607182418800017408]
 [                  0]]
<class 'numpy.ndarray'>
(4, 1)
int64

By lepiej zrozumieć kształt n-wymiarowych tablic, przestudiujmy poniższe zdjęcie:

import matplotlib.pyplot as plt
import cv2
from google.colab import drive
from google.colab.patches import cv2_imshow
drive.mount('/content/drive')
image = cv2.imread('/content/drive/My Drive/Warsztaty/axes.png')
cv2_imshow(image)

Mounted at /content/drive

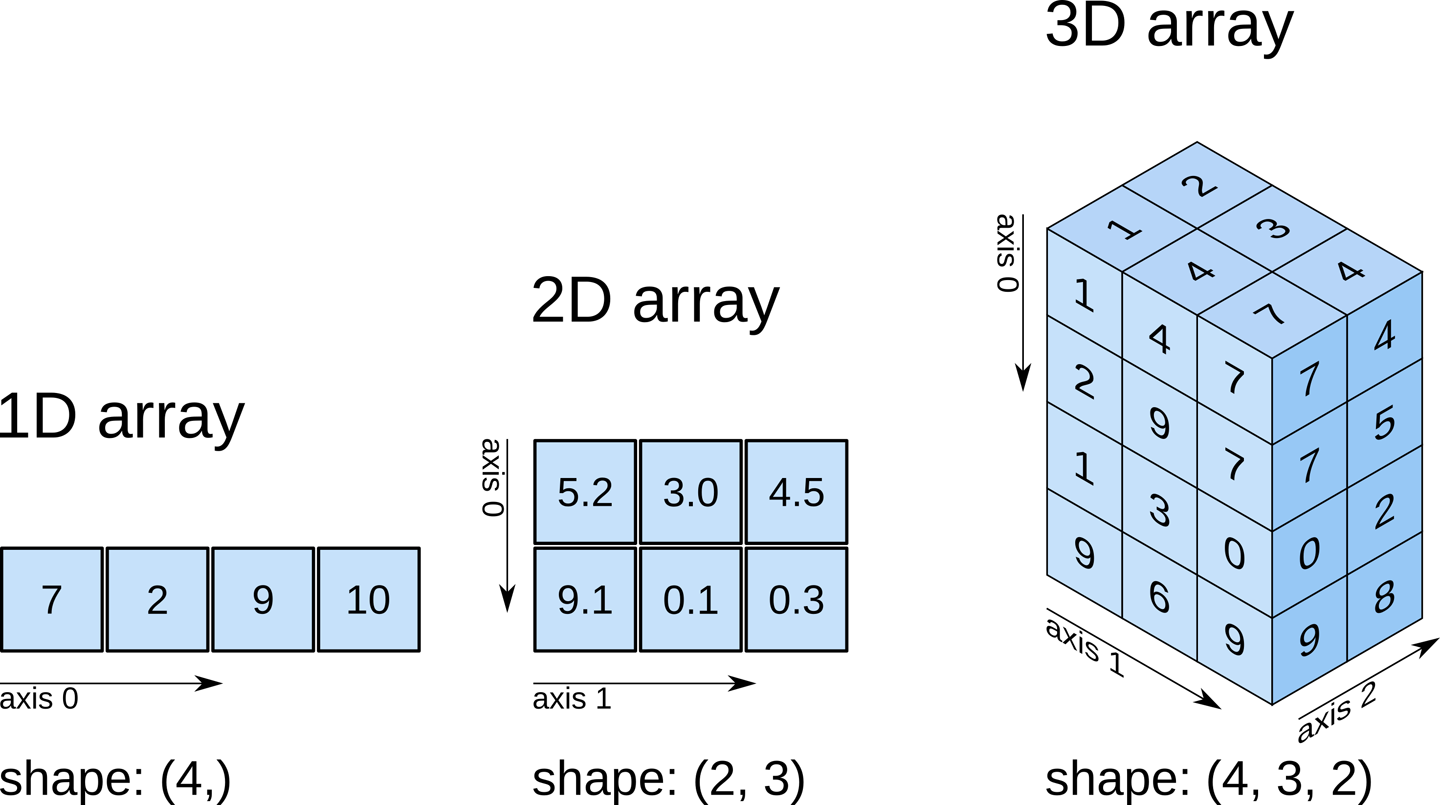
Wymiary w ndarray nazywane są axes (l. poj. axis).

Jakie wymiary będą miały poniższe przykłady?

import numpy as np
ex_1 = np.array([[ 1., 0., 0.],[ 0., 1., 2.]])
ex_2 = np.array([[1, 1]])
ex_3 = np.array([[]])
ex_4 = np.array([1, 2, 3])
ex_5 = np.array([])
ex_6 = np.array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

print(ex_1.shape)
print(ex_2.shape)
print(ex_3.shape)
print(ex_4.shape)
print(ex_5.shape)
print(ex_6.shape)

(2, 3)
(1, 2)
(1, 0)
(3,)
(0,)
(3, 5)

Dodatkowe parametry:

ndim - zwraca liczbę axes, wymiarów

size - zwraca liczbę elementów w tablicy

Przykład:

nd_arr = np.array([[ 0,  1,  2,  3,  4],
                   [ 5,  6,  7,  8,  9],
                   [10, 11, 12, 13, 14]])
print(nd_arr.shape)
print(nd_arr.ndim)
print(nd_arr.size)

(3, 5)
2
15

3. Podstawowe operacje na tablicach wielowymiarowych

Operacje arytmetyczne

Operacje arytmetyczne są zawsze wykonywane elementwise (na poszczególnych elementach)

'''
Przykład wykorzystany w książce Uczenie maszynowe z użyciem Scikit-Learn i TensorFlow Helion 2018
'''
import numpy as np
import matplotlib.pyplot as plt # biblioteka wykorzystywana do tworzenia wykresów, więcej powiemy o niej później

u = np.array([5, 2])
v = np.array([1, 6])

''' 
Funkcja odpowiadająca za narysowanie strzałki wskazującej pozycję wektora od początku
Domyślnie początek jest ustawiony na koordynaty (0, 0)
'''
def rysuj_wektor(wektor, poczatek=[0, 0], **options): 
    return plt.arrow(poczatek[0], poczatek[1], wektor[0], wektor[1],
              head_width=0.3, head_length=0.4, length_includes_head=True,
              **options)

rysuj_wektor(u, color="r")
rysuj_wektor(v, color="b")
plt.axis([0, 6, 0, 7])
plt.grid()
plt.text(2.5, 1.2, "u", color="r", fontsize=18)
plt.text(0.3, 3.5, "v", color="b", fontsize=18)
plt.show()

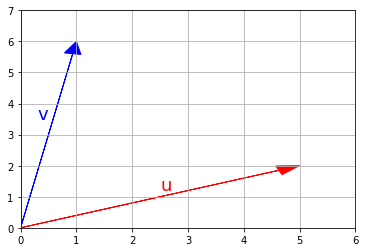
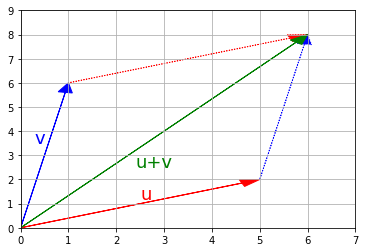
Dodawanie

\[c_{ij} = a_{ij} + b_{ij}\]

\[A_{m,n} + B_{m,n} =\begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} + \begin{pmatrix} b_{1,1} & \cdots & b_{1,n} \\ \vdots & \ddots & \vdots \\ b_{m,1} & \cdots & b_{m,n} \end{pmatrix} = \begin{pmatrix} a_{1,1} + b_{1,1} & \cdots & a_{1,n} + b_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} + b_{m,1} & \cdots & a_{m, n} + b_{m,n} \end{pmatrix}\]

Przykłady:

rysuj_wektor(u, color="r")
rysuj_wektor(v, color="b")
rysuj_wektor(v, poczatek=u, color="b", linestyle="dotted")
rysuj_wektor(u, poczatek=v, color="r", linestyle="dotted")
rysuj_wektor(u+v, color="g")
plt.axis([0, 7, 0, 9])
plt.text(2.5, 1.2, "u", color="r", fontsize=18)
plt.text(0.3, 3.5, "v", color="b", fontsize=18)
plt.text(2.4, 2.5, "u+v", color="g", fontsize=18)
plt.grid()
plt.show()

a = np.array( [20,30,40,50] )
b = np.array( [0, 1, 2, 3,] )
c = a + b
print(c)

[20 31 42 53]

a = np.array( [[5,10],[-3, 0]])
b = np.array( [[7, 2], [2, 3,]] )
c = a + b
print(c)

[[12 12]
 [-1  3]]

Odejmowanie

\[c_{ij} = a_{ij} - b_{ij}\]

\[A_{m,n} - B_{m,n} =\begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} - \begin{pmatrix} b_{1,1} & \cdots & b_{1,n} \\ \vdots & \ddots & \vdots \\ b_{m,1} & \cdots & b_{m,n} \end{pmatrix} = \begin{pmatrix} a_{1,1} - b_{1,1} & \cdots & a_{1,n} - b_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} - b_{m,1} & \cdots & a_{m, n} - b_{m,n} \end{pmatrix}\]

Przykłady:

a = np.array( [20,30,40,50] )
b = np.array( [0, 1, 2, 3,] )
c = a - b
print(c)

[20 29 38 47]

a = np.array( [[5,10],[-3, 0]])
b = np.array( [[7, 2], [2, 3,]] )
c = a - b
print(c)

[[-2  8]
 [-5 -3]]

Mnożenie przez skalar

\[c_{ij} = a_{ij} \cdot r\]

\[(rA_{m,n})=r\cdot\begin{pmatrix} a_{1,1} & \cdots & a_{1,n} \\ \vdots & \ddots & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} = \begin{pmatrix} r\cdot a_{1,1} & \cdots & r\cdot a_{1,n}\\ \vdots & \ddots & \vdots \\ r\cdot a_{m,1} & \cdots & r\cdot a_{m, n} \end{pmatrix}\]

Przykłady:

a = np.array( [20,30,40,50] )
r = 10
c = a*r
print(c)

[200 300 400 500]

a = np.array( [[1, 2, 3],[4, 5, 6]] )
r = 0.25
c = a*r
print(c)

[[0.25 0.5  0.75]
 [1.   1.25 1.5 ]]

a = np.array( [[10, 20],[30, 40]] )
r = 10
c = a/r # dzielenie macierzy = mnożenie przez odwrotność
print(c)

[[1. 2.]
 [3. 4.]]

Mnożenie tablic

Trzeba szczególnie uważać na mnożenie tablic między sobą.

Domyślna operacja

*

Zwróci nam następujące wartości

\[c_{ij} = a_{ij} \cdot b_{ij}\]

Przykład:

a = np.array( [20,30,40,50] )
b = np.array( [0, 1, 2, 3] )
c = a * b
print(c)

[  0  30  80 150]

Gdy interesuje nas mnożenie Cauchy’ego zdefiniowane w następujący sposób:

\[c_{i,j}=\sum_{r=1}^m a_{i,r}b_{r,i}\]

Musimy użyć funkcji

np.matmul(pierwsza_macierz, druga_macierz)

bądź operatora

@

Działanie to zdefiniowane jest wyłącznie dla macierzy, z których pierwsza ma tyle kolumn, co druga wierszy.

Przykład:

a = np.array( [[1,2],[3,0]] )
b = np.array( [[0, 1], [2, 3]] )
c = a @ b
print(c)
c = np.matmul(a,b)
print(c)

[[4 7]
 [0 3]]
[[4 7]
 [0 3]]

a = np.array( [[1,2]] )
b = np.array( [[0, 1], [2, 3]] )
c = b@a
print(c)

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

<ipython-input-109-9cab40bd7661> in <module>()
      1 a = np.array( [[1,2]] )
      2 b = np.array( [[0, 1], [2, 3]] )
----> 3 c = b@a
      4 print(c)


ValueError: matmul: Input operand 1 has a mismatch in its core dimension 0, with gufunc signature (n?,k),(k,m?)->(n?,m?) (size 1 is different from 2)

Nakładanie funkcji na tablice

Numpy umożliwia nakładanie funkcji na każdy element tablicy

Przykład

a = np.array( [0, 1, 2, 3] )
b = a**2 # potęgowanie
print(b)

[0 1 4 9]

a = np.array( [0, np.pi/2, np.pi, 3/2*np.pi] )
b = np.round(np.sin(a)) # wyliczanie sinusa i zaokrągranie wartości
print(b)

[ 0.  1.  0. -1.]

import numpy as np
a = np.array( [20,30,40,50] )
print(a.max()) # znajduje maksymalną wartość
print(a.min()) # znajduje minimalną wartość
print(a.sum()) # sumuje wartości
print(a.prod()) # zwraca iloczyn
print(a.mean()) # zwraca średnią
print(a.std()) # zwraca odchylenie standardowe
print(a.var()) # zwraca wariancję

50
20
140
1200000
35.0
11.180339887498949
125.0

W przypadku tablicy wielowymiarowej często trzeba określić względem jakiego wymiaru operacje mają się wykonywać

b = np.array([[ 0,  1,  2,  3],
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])

print(b.sum(axis=0))
print(b.sum(axis=1))

[12 15 18 21]
[ 6 22 38]

Więcej funkcji można znaleźć tutaj

Funkcje tworzące tablice

Numpy umożliwia wiele możliwości tworzenia tablic wypełnionymi konkretnymi danymi

Funkcja

zeros

tworzy tablice pełną zer.

Funkcja

ones

tworzy tablicę pełną jedynek.

Funkcja

empty

tworzy tablicę której zainicjalizowana wartość jest losowa, zależna od tego co jest przechowywane w pamięci.

Wymiary tablicy muszą być podawane w nawiasach!

np.zeros((wymiar1, wymiar2), dtype=typ)

Domyślnie dtype wszystkich tych funkcji jest floatem (liczby zmiennoprzecinkowe), ale można go zdefiniować oraz podać ilość obiektów w jednej komórce.

Przykład:

np.zeros( (3,4) )

array([[0., 0., 0., 0.],
       [0., 0., 0., 0.],
       [0., 0., 0., 0.]])

np.ones( (3,4), dtype=int)

array([[1, 1, 1, 1],
       [1, 1, 1, 1],
       [1, 1, 1, 1]])

np.empty( (3,4) )

array([[5.97074934e-316, 0.00000000e+000, 4.11556683e-321,
        1.59254195e-316],
       [6.92303567e-310, 6.92303567e-310, 6.92303567e-310,
        6.92303567e-310],
       [0.00000000e+000, 2.96439388e-323, 2.12199579e-314,
        6.92303731e-310]])

a = np.zeros( (1,2), dtype=(int,2))
print(a) # w każdej komórce przechowywane są dwa obiekty typu int
print(a.shape) # zwróćmy uwagę na wymiary!

[[[0 0]
  [0 0]]]
(1, 2, 2)

Jeżeli chcemy zainicjować tablice wartościami z pewnego przedziału możemy wykorzystać funkcję

arange

będącą funkcją zbliżoną do funkcji range w Pythonie

np.arange(od, do, krok)

Przykład:

print(np.arange( 10, 30, 5 ))
print(np.arange(6))

[10 15 20 25]
[0 1 2 3 4 5]

Bądź funkcję

linspace

która zwraca n liczb z pewnego przedziału z równym odstępem (w tym przypadku początek jak i koniec są domknięte)

np.linspace(od, do, ile_liczb)

Przykład:

np.linspace( 0, 2, 9 )

array([0.  , 0.25, 0.5 , 0.75, 1.  , 1.25, 1.5 , 1.75, 2.  ])

Jeżeli chcemy uzupełnić tablicę wartościami pseudolosowymi zastosujemy funkcję random

np.random.random((wymiar1, wymiar2))

zwracającą wartości z przedziału 0 - 1 Przykład:

np.random.random((2,3))

array([[0.72096784, 0.15166739, 0.62780155],
       [0.14470733, 0.5110661 , 0.3135805 ]])

Funkcje modyfikujące wymiary tablicy

Inną, dość częstą operacją jaką będziemy stosować na naszej tablicy to zmiana jej wymiarów.

Do zmiany wymiarów tablicy wykorzystywana jest funkcja

reshape

która jako parametr otrzymuje nowe wymiary tablicy

n_wym_tablica.reshape(nowe_wymiary)

Przykład:

a = np.arange(12)
print(a)
print(a.shape)
a = a.reshape(3,4)
print(a)
print(a.shape)

[ 0  1  2  3  4  5  6  7  8  9 10 11]
(12,)
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)

Do spłaszczenia tablicy do jednego wymiaru służy funkcja

ravel

np.ravel(tablica_do_spłaszczenia)

Przykład:

print(a)
print(a.shape)
print(np.ravel(a))
print(np.ravel(a).shape)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
(3, 4)
[ 0  1  2  3  4  5  6  7  8  9 10 11]
(12,)

Bardzo często przy pracy na macierzach interesuje nas transpozycja macierzy.

Do dokonania transpozycji służy funkcja

transpose

albo parametr

T

Przykład:

a = np.arange(15).reshape(3,5)
print(a)
print(a.shape)
print(a.T)
print(a.T.shape)
b = a.transpose()
print(b)
print(b.shape)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]
(3, 5)
[[ 0  5 10]
 [ 1  6 11]
 [ 2  7 12]
 [ 3  8 13]
 [ 4  9 14]]
(5, 3)
[[ 0  5 10]
 [ 1  6 11]
 [ 2  7 12]
 [ 3  8 13]
 [ 4  9 14]]
(5, 3)

4. Algebra liniowa

Pakiet numpy posiada całkiem zaawansowaną część poświęconą algebrze liniowej.

Wprawa w tej dziedzinie (chociażby na poziomie podstawowym) jest konieczna w analizie danych. Wiele operacji, algorytmów wykonywanych jest na macierzach w celu przyspieszenia czasu wykonywania.

Rozpiskę wszystkich funkcji oferowanych przez numpy dotyczących algebry liniowej można znaleźć tutaj

Norma

Norma wektora \(\textbf{u}\), zapisywana jako \(\left \Vert \textbf{u} \right \|\), stanowi miarę długośc (tzn. modułu) wektora \(\textbf{u}\). Istnieje wiele różnych norm, najczęściej jednak stosowaną jest norma euklidesowa, definiowana jako:

\[\left \Vert \textbf{u} \right \| = \sqrt{\sum_{i}{\textbf{u}_i}^2}\]

def norma_wektora(wektor): # własnoręcznie napisana funkcja do wyliczania normy
    return sum([element**2 for element in wektor])**0.5

u = np.array([3, 4])

print(norma_wektora(u))

5.0

Możemy też wykorzystać do tego problemu bibliotekę Numpy, a dokładniej metodę

numpy.linalg.norm(wektor)

import numpy.linalg as LA
LA.norm(u)

5.0

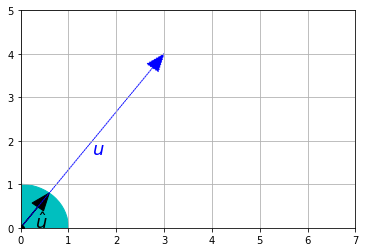
Wektor znormalizowany wektora niezerowego \(\textbf{u}\), zapisywany jako \(\hat{\textbf{u}}\), jest wektorem jednostkowym skierowanym w tę samą stronę, co wektor \(\textbf{u}\). Jest on równy:

\[\hat{\textbf{u}} = \dfrac{\textbf{u}}{\left \Vert \textbf{u} \right \|}\]

plt.gca().add_artist(plt.Circle((0,0),1,color='c'))
plt.plot(0, 0, "ko")
rysuj_wektor(u / LA.norm(u), color="k")
rysuj_wektor(u, color="b", linestyle=":")
plt.text(0.3, 0, "$\hat{u}$", color="k", fontsize=18)
plt.text(1.5, 1.7, "$u$", color="b", fontsize=18)
plt.axis([0, 7, 0, 5])
plt.grid()
plt.show()

Iloczyn skalarny

(ang. dot product) definiujemy w następujący sposób:

\[\textbf{u} \cdot \textbf{v} = \left \Vert \textbf{u} \right \| \times \left \Vert \textbf{v} \right \| \times cos(\theta)\]

gdzie:

\(\theta\) - kąt pomiędzy wektorami \(\textbf{u}\) i \(\textbf{v}\).

Możemy obliczyć go przy pomocy poniższego polecenia

np.dot(wektor1, wektor2)

u = np.array([2, 0])
v = np.array([4, 0])

rysuj_wektor(u, color="k")
rysuj_wektor(v, color="b", linestyle=":")
rysuj_wektor([np.dot(u,v),0], color="r")
plt.text(0.3, 0.1, "$u$", color="k", fontsize=18)
plt.text(2.5, 0.1, "$v$", color="b", fontsize=18)
plt.text(4.5, 0.1, "$u \cdot v$", color="r", fontsize=18)
plt.axis([0, 8, -2, 2])
plt.grid()
plt.show()

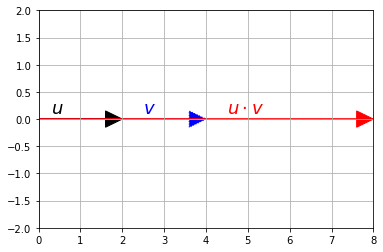
print(np.dot(u,v))

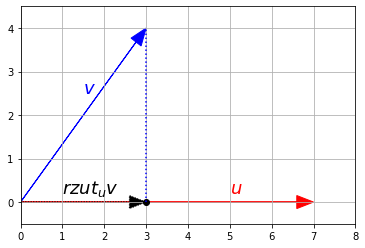
Rzutowanie punktu na oś

Iloczyn skalarny jest również używany do rzutowania punktów na oś. Rzutowanie wektora \(\textbf{v}\) na oś \(\textbf{u}\) jest przeprowadzane za pomocą następującego równania:

\[\textbf{proj}_{\textbf{u}}{\textbf{v}} = \dfrac{\textbf{u} \cdot \textbf{v}}{\left \Vert \textbf{u} \right \| ^2} \times \textbf{u}\]

Co jest równoważne wzorowi:

\[\textbf{proj}_{\textbf{u}}{\textbf{v}} = (\textbf{v} \cdot \hat{\textbf{u}}) \times \hat{\textbf{u}}\]

u = np.array([7, 0])
v = np.array([3, 4])

u_normalized = u / LA.norm(u)
proj = np.dot(v, u_normalized) * u_normalized

rysuj_wektor(u, color="r")
rysuj_wektor(v, color="b")

rysuj_wektor(proj, color="k", linestyle=":")
plt.plot(proj[0], proj[1], "ko")

plt.plot([proj[0], v[0]], [proj[1], v[1]], "b:")

plt.text(1, 0.2, "$rzut_u v$", color="k", fontsize=18)
plt.text(1.5,2.5, "$v$", color="b", fontsize=18)
plt.text(5, 0.2, "$u$", color="r", fontsize=18)

plt.axis([0, 8, -0.5, 4.5])
plt.grid()
plt.show()

Obliczanie kąta pomiędzy wektorami

Jednym z wielu zastosowań iloczynu skalarnego jest obliczanie kąta pomiędzy dwoma niezerowymi wektorami. Za pomocą definicji iloczynu skalarnego możemy wyznaczyć następujący wzór:

\[\theta = \arccos{\left ( \dfrac{\textbf{u} \cdot \textbf{v}}{\left \Vert \textbf{u} \right \| \times \left \Vert \textbf{v} \right \|} \right ) }\]

Jeśli \(\textbf{u} \cdot \textbf{v} = 0\), to \(\theta = \dfrac{π}{2}\). Innymi słowy, jeśli iloczyn skalarny dwóch niezerowych wektorów jest równy 0, to znaczy, że są one prostopadłe względem siebie.

Skorzystajmy z tego wzoru do obliczenia kąta pomiędzy wektorami \(\textbf{u}\) i \(\textbf{v}\) (w radianach):

def kat_wektora(u, v):
    cos_theta = np.dot(u,v) / (LA.norm(u) * LA.norm(v))
    return np.arccos(np.clip(cos_theta, -1, 1))

u = np.array([2, 5])
v = np.array([3, 1])

theta = kat_wektora(u, v)
print("Kąt =", theta, "radianów")
print("      =", theta * 180 / np.pi, "stopni")

Kąt = 0.8685393952858896 radianów
      = 49.76364169072618 stopni

Macierze

Macierz diagonalna

Macierz diagonalną, na przykład:

\[\begin{bmatrix} 4 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 6 \end{bmatrix}\]

możemy stworzyć za pomocą funkcji:

np.diag(lista elementów mających pojawić się na głównej przekątnej)

print(np.diag(np.array([1,2,3])))

[[1 0 0]
 [0 2 0]
 [0 0 3]]

Jeśli zaś przekażemy macierz do funkcji diag, zostaną wypisane elementy znajdujące się w głównej przekątnej:

D = np.array([
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9],
    ])
np.diag(D)

array([1, 5, 9])

Macierz jednostkowa

Macierz jednostkową (tożsamościową) o rozmiarze n definiujemy w następujący sposób.

np.eye(n)

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

print(np.eye(3))

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

Macierz transponowana

Transpozycją macierzy \(M\) nazywamy macierz zapisywaną jako \(M^T\), w której \(i^{ty}\) rząd jest równy \(i^{tej}\) kolumnie macierzy \(M\):

\[A^T = \begin{bmatrix} 10 & 20 & 30 \\ 40 & 50 & 60 \end{bmatrix}^T = \begin{bmatrix} 10 & 40 \\ 20 & 50 \\ 30 & 60 \end{bmatrix}\]

Innymi słowy (\(A^T)_{i,j}\) = \(A_{j,i}\)

Oczywiście, jeśli macierz \(M\) ma rozmiar \(m \times n\), to jej transpozycja \(M^T\) przyjmuje postać \(n \times m\).

Macierz transponowaną za pomocą atrybutu T

macierz.T

bądź funkcji

np.transpose(macierz)

która dodatkowo potrafi określić względem jakich osi ma zostać wykonana permutacja macierzy

A = np.array([[10, 20, 30],[40, 50, 60]])

print('='*20)
print('atrybut T')
print('='*20)
print(A)
print('-'*20)
print(A.T)
print('-'*20)
print(A.T.T)
print('='*20)
print('funkcja transpose()')
print('='*20)
print(A)
print('-'*20)
print(np.transpose(A))
print('-'*20)
print(np.transpose(np.transpose(A)))
print('-'*20)

====================
atrybut T
====================
[[10 20 30]
 [40 50 60]]
--------------------
[[10 40]
 [20 50]
 [30 60]]
--------------------
[[10 20 30]
 [40 50 60]]
====================
funkcja transpose()
====================
[[10 20 30]
 [40 50 60]]
--------------------
[[10 40]
 [20 50]
 [30 60]]
--------------------
[[10 20 30]
 [40 50 60]]
--------------------

Graficzne przedstawianie macierzy

Wektory mogą być reprezentowane jako punkty lub strzałki w N-wymiarowej przestrzeni. Jeżeli uznamy macierze za listy wektorów, to jej wykresem jest określona liczba punktów lub strzałek. Stwórzmy, na przykład, macierz \(P\) o rozmiarze \(2 \times 4\) i wygenerujmy jej wykres w postaci punktów:

import matplotlib.pyplot as plt

P = np.array([
        [3.0, 4.0, 1.0, 4.6],
        [0.2, 3.5, 2.0, 0.5]
    ])
x_coords_P, y_coords_P = P
plt.scatter(x_coords_P, y_coords_P)
plt.axis([0, 5, 0, 4])
plt.show()

Zastosowania geometryczne operacji macierzowych

Dodawanie wektorów skutkuje procesem translacji geometrycznej, mnożenie wektorów przez skalar zmnienia skalę (powiększa lub pomniejsza, gdzie środek stanowi początek układu współrzędnych), natomiast iloczyn wektorowy skutkuje rzutowaniem wektora na inny wektor, co powoduje przeskalowanie i pomiar wynikowej współrzędnej.

Również operacje macierzowe mają bardzo użyteczne zastosowania geometryczne.

Dodawanie macierzy

from matplotlib.patches import Polygon

H = np.array([
        [ 0.5, -0.2, 0.2, -0.1],
        [ 0.4,  0.4, 1.5, 0.6]
    ])
P_moved = P + H

plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_moved.T, alpha=0.3, color="r"))
for vector, origin in zip(H.T, P.T):
    rysuj_wektor(vector, poczatek=origin)

plt.text(2.2, 1.8, "$P$", color="b", fontsize=18)
plt.text(2.0, 3.2, "$P+H$", color="r", fontsize=18)
plt.text(2.5, 0.5, "$H_{*,1}$", color="k", fontsize=18)
plt.text(4.1, 3.5, "$H_{*,2}$", color="k", fontsize=18)
plt.text(0.4, 2.6, "$H_{*,3}$", color="k", fontsize=18)
plt.text(4.4, 0.2, "$H_{*,4}$", color="k", fontsize=18)

plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()

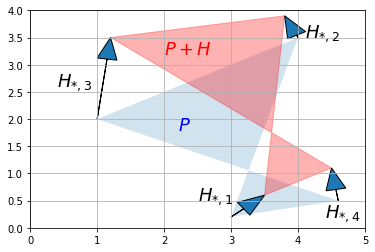
Dodanie macierzy wypełnionej identycznymi wektorami skutkuje prostą translacją geometryczną

H2 = np.array([
        [-0.5, -0.5, -0.5, -0.5],
        [ 0.4,  0.4,  0.4,  0.4]
    ])
P_translated = P + H2

plt.gca().add_artist(Polygon(P.T, alpha=0.2))
plt.gca().add_artist(Polygon(P_translated.T, alpha=0.3, color="r"))
for vector, origin in zip(H2.T, P.T):
    rysuj_wektor(vector, poczatek=origin)

plt.axis([0, 5, 0, 4])
plt.grid()
plt.show()

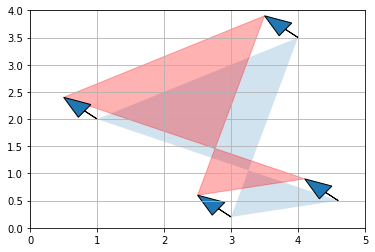
Mnożenie przez skalar

def rysuj_translacje(P_przed, P_po, tekst_przed, tekst_po, axis = [0, 5, 0, 4], arrows=False):
    if arrows:
        for wektor_przed, wektor_po in zip(P_przed.T, P_po.T):
            rysuj_wektor(wektor_przed, color="blue", linestyle="--")
            rysuj_wektor(wektor_po, color="red", linestyle="-")
    plt.gca().add_artist(Polygon(P_przed.T, alpha=0.2))
    plt.gca().add_artist(Polygon(P_po.T, alpha=0.3, color="r"))
    plt.text(P_przed[0].mean(), P_przed[1].mean(), tekst_przed, fontsize=18, color="blue")
    plt.text(P_po[0].mean(), P_po[1].mean(), tekst_po, fontsize=18, color="red")
    plt.axis(axis)
    plt.grid()

P_przeskalowane = 0.60 * P
rysuj_translacje(P, P_przeskalowane, "$P$", "$0.6 P$", arrows=True)
plt.show()

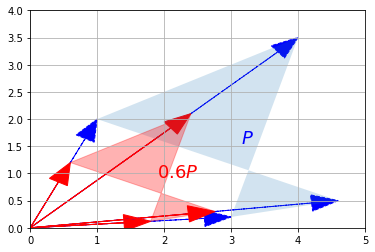
Przekształcenia liniowe

W bardziej ogólnym ujęciu każde przekształcenie liniowe \(f\) odwzorowujące n-wymiarowe wektory na m-wymiarowe wektory możemy przedstawiać za pomocą macierzy. Załóżmy, na przykład, że mamy do czynienia z trójwymiarowym wektorem \(\textbf{u}\):

\[\textbf{u} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\]

a przekształcenie \(f\) definiujemy jako:

\[f(\textbf{u}) = \begin{pmatrix} ax + by + cz \\ dx + ey + fz \end{pmatrix}\]

Transformacja ta odwzorowuje trójwymiarowe wektory do postaci dwuwymiarowej w sposób liniowy (tzn. otrzymywane współrzędne stanowią jedynie sumy iloczynów pierwotnych koordynatów). Możemy zapisać to przekształcenie jako macierz \(F\):

\[F = \begin{bmatrix} a & b & c \\ d & e & f \end{bmatrix}\]

Teraz w celu obliczenia \(f(\textbf{u})\) wystarczy przeprowadzić mnożenie macierzowe:

\[f(\textbf{u}) = F \textbf{u}\]

Jeśli mamy macierz \(G = \begin{bmatrix}\textbf{u}_1 & \textbf{u}_2 & \cdots & \textbf{u}_q \end{bmatrix}\), gdzie każdy element \(\textbf{u}_i\) stanowi trójwymiarowy wektor kolumnowy, to operacja \(FG\) spowoduje liniowe przekształcenie wszystkich wektorów \(\textbf{u}_i\) w sposób zdefiniowany w macierzy \(F\):

\[FG = \begin{bmatrix}f(\textbf{u}_1) & f(\textbf{u}_2) & \cdots & f(\textbf{u}_q) \end{bmatrix}\]

Podsumowując, macierz znajdująca się po lewej stronie iloczynu wektorowego określa stosowane przekształcenie liniowe wobec wektorów znajdujących się po prawej stronie.

Przykład

Zdefiniujmy macierz, która będzie reprezentowana przez kwadrat jednostkowy

kwadrat = np.array([
        [0, 0, 1, 1],
        [0, 1, 1, 0]
    ])

plt.gca().add_artist(Polygon(kwadrat.T, alpha=0.2))
plt.axis([0, 2, 0, 2])
plt.show()

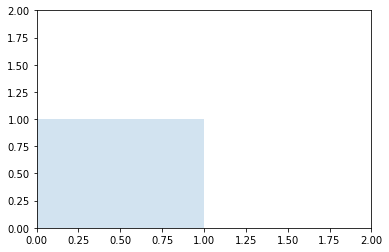
Mnożenie przez macierz jednostkową

nie zmienia właściwości macierzy

\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 0 & 0 & 1 & 1\\ 0 & 1 & 1 & 0 \end{bmatrix} =\begin{bmatrix} 0 & 0 & 1 & 1\\ 0 & 1 & 1 & 0 \end{bmatrix}\]

macierz_jednostkowa = np.eye(2)
plt.gca().add_artist(Polygon(np.dot(macierz_jednostkowa, kwadrat).T, alpha=0.2))
plt.axis([0, 2, 0, 2])
plt.show()

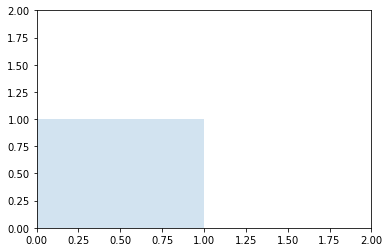
Skalowanie

\[\begin{bmatrix} szerokość & 0 \\ 0 & wysokość \end{bmatrix}\]

szerokość = 2
wysokość = 2
skalowanie = np.array([[szerokość, 0],[0, wysokość]])

plt.gca().add_artist(Polygon(np.dot(skalowanie, kwadrat).T, alpha=0.2))
plt.axis([0, 2, 0, 2])
plt.show()

Rotacja

\[\begin{bmatrix} \cos{\phi} & \sin{\phi} \\ -\sin{\phi} & \cos{\phi} \end{bmatrix}\]

gdzie

\(\phi\) - kąt o jaki chcemy obrócić macierz względem osi OY

rotacja = np.array([[np.cos(np.pi/6), np.sin(np.pi/6)],[-1*np.sin(np.pi/6), np.cos(np.pi/6)]])

plt.gca().add_artist(Polygon(np.dot(rotacja, kwadrat).T, alpha=0.2))
plt.axis([0, 2, -0.5, 2])
plt.show()

Powinowactwo osiowe

Względem osi X

\[\begin{bmatrix} 1 & \tan{\phi} \\ 0 & 1 \end{bmatrix}\]

Względem osi Y

\[\begin{bmatrix} 1 & 0 \\ \tan{\psi} & 1 \end{bmatrix}\]

gdzie

\(\phi\) - kąt o jaki przesunięty zostanie część macierzy względem osi OY
\(\psi\) - kąt o jaki przesunięty zostanie część macierzy względem osi OX

powinowactwo_x = np.array([[1, np.tan(np.pi/6)],[0, 1]])

plt.gca().add_artist(Polygon(np.dot(powinowactwo_x, kwadrat).T, alpha=0.2))
plt.axis([0, 2, 0, 2])
plt.show()

powinowactwo_y = np.array([[1, 0],[np.tan(np.pi/6), 1]])

plt.gca().add_artist(Polygon(np.dot(powinowactwo_y, kwadrat).T, alpha=0.2))
plt.axis([0, 1.5, 0, 2])
plt.show()

Odbicie

Względem początku

\[\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}\]

Względem osi X

\[\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\]

Względem osi Y

\[\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\]

odbicie_x = np.array([[1, 0],[0, -1]])

plt.gca().add_artist(Polygon(np.dot(odbicie_x, kwadrat).T, alpha=0.2))
plt.axis([-1, 1, -1, 1])
plt.show()

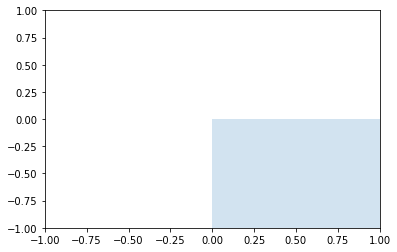
odbicie_y = np.array([[-1, 0],[0, 1]])

plt.gca().add_artist(Polygon(np.dot(odbicie_y, kwadrat).T, alpha=0.2))
plt.axis([-1, 1, -1, 1])
plt.show()

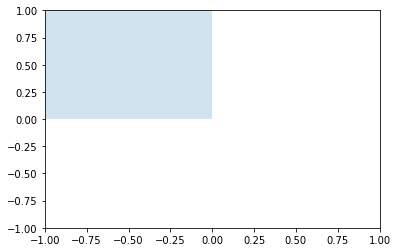
odbicie_pocz = np.array([[-1, 0],[0, -1]])

plt.gca().add_artist(Polygon(np.dot(odbicie_pocz, kwadrat).T, alpha=0.2))
plt.axis([-1, 1, -1, 1])
plt.show()

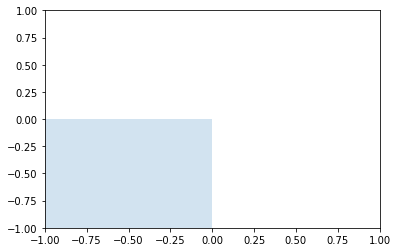
Macierz odwrotna

Macierz może reprezentować dowolne przekształcenie liniowe, może więc pojawić się w naszych głowach pytanie: czy istnieje macierz transformacji odwracająca efekt danej macierzy transformacji \(F\)?

Odpowiedź brzmi: tak… czasami! Jeśli taka macierz istnieje, jest ona nazywana macierzą odwrotną i zapisujemy ją jako \(F^{-1}\).

By ją wyliczyć możemy skorzystać z funkcji

numpy.linalg.inv(macierz_kwadratowa)

Jeżeli podana macierz jest nie prawidłowa, bądź nie istnieje macierz odwrotna do podanej zostanie wyrzucony wyjątek

LinAlgError

import numpy.linalg as LA

wynik_przeksztalcenia = np.dot(odbicie_pocz, kwadrat)

try:
  macierz_odwrotna = LA.inv(odbicie_pocz)
  plt.gca().add_artist(Polygon(np.dot(macierz_odwrotna, wynik_przeksztalcenia).T, alpha=0.2))
  plt.axis([-1, 1, -1, 1])
  plt.show()
except LA.LinAlgError as lae:
  print("Nie udało się znaleźć macierzy odwrotnej, informacje o błędach: " + str(lae))

Wyznacznik

Wyznacznikiem macierzy kwadratowej \(M\), zapisywanym jako \(\det(M)\) lub \(\det M\) albo \(|M|\), nazywamy wartość wyliczaną z jej elementów \((M_{i,j})\) za pomocą różnych równoznacznych metod. Jedną z najprostszych metod jest podejście rekurencyjne:

\[|M| = M_{1,1}\times|M^{(1,1)}| - M_{2,1}\times|M^{(2,1)}| + M_{3,1}\times|M^{(3,1)}| - M_{4,1}\times|M^{(4,1)}| + \cdots ± M_{n,1}\times|M^{(n,1)}|\]

gdzie \(M^{(i,j)}\) jest macierzą \(M\) bez rzędu \(i\) i kolumny \(j\).

Na przykład, obliczmy wyznacznik następującej macierzy o rozmiarze \(3 \times 3\):

\[M = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 0 \end{bmatrix}\]

Za pomocą powyższej metody uzyskujemy:

\[|M| = 1 \times \left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | - 2 \times \left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | + 3 \times \left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right |\]

Teraz musimy obliczyć wyznacznik każdej z tych macierzy o rozmiarze \(2 \times 2\) (wyznaczniki te są nazywane minorami):

\[\left | \begin{bmatrix} 5 & 6 \\ 8 & 0 \end{bmatrix} \right | = 5 \times 0 - 6 \times 8 = -48\] \[\left | \begin{bmatrix} 4 & 6 \\ 7 & 0 \end{bmatrix} \right | = 4 \times 0 - 6 \times 7 = -42\] \[\left | \begin{bmatrix} 4 & 5 \\ 7 & 8 \end{bmatrix} \right | = 4 \times 8 - 5 \times 7 = -3\]

A teraz czas obliczyć ostateczny wynik:

\[|M| = 1 \times (-48) - 2 \times (-42) + 3 \times (-3) = 27\]

Wyznaczanie wyznaczników macierzy (szczególnie większych rozmiarów) jest wyjątkowo żmudnym zadaniem, w którym bardzo łatwo popełnić błąd.

Na ratunek przybywa numpy oraz funkcja

numpy.linalg.det(macierz)

M = np.array([
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 0]
    ])
LA.det(M)

27.0

M = np.array([
        [2, 2, 3, 4, 5, 6],
        [7, 8, 9, 10, 11, 12],
        [13, 14, 0, 16, 17, 18],
        [19, 20, 21, 22, 23, 24],
        [25, 26, 27, 28, 0, 30],
        [31, 32, 33, 34, 35, 0],             
])
print(M)
print(LA.det(M))

[[ 2  2  3  4  5  6]
 [ 7  8  9 10 11 12]
 [13 14  0 16 17 18]
 [19 20 21 22 23 24]
 [25 26 27 28  0 30]
 [31 32 33 34 35  0]]
375840.0000000006

Wektory własne i wartości własne

Wektorem własnym (zwanym także wektorem charakterystycznym) macierzy kwadratowej \(M\) nazywamy wektor niezerowy niezmieniający swojego kierunku po przekształceniu liniowym zdefiniowanym przez macierz \(M\). Zgodnie z bardziej formalną definicją jest to dowolny wektor \(v\), który

\[M \cdot v = \lambda \times v\]

gdzie \(\lambda\) jest wielkością skalarną zwaną wartością własną, powiązaną z wektorm \(v\).

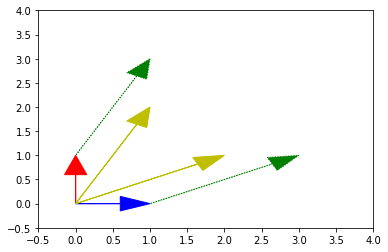
Na przykład każdy wektor poziomy pozostaje taki po zastosowaniu powinowactwa osiowego (co widać na poniższym wykresie), zatem jest on wektorem własnym przekształcenia \(M\). Wektor pionowy zostaje nieco przechylony w prawo, zatem wektory pionowe NIE SĄ wektorami własnymi macierzy \(M\).

Funkcja

numpy.linalg.eig(macierz_kwadratowa)

modułu NumPy zwraca listę jednostkowych wektorów własnych i odpowiadające im wartości własne dla dowolnej macierzy kwadratowej.

Zadanie z egzaminu

Wyznaczyć wartości własne i wektory własne przekształcenia liniowego \(\phi: \mathbb{R}^2 \rightarrow \mathbb{R}^2, \phi(x,y) = (2x+y, x+2y)\)

baza = [[1,0],[0,1]]
PHI = np.array([[2, 1],[1, 2]])
wynik = np.dot(PHI, baza)

print(wynik)

rysuj_wektor(baza[0], color="b")
rysuj_wektor(baza[1], color="r")
rysuj_wektor(wynik[0], color='y')
rysuj_wektor(wynik[1], color='y')
rysuj_wektor(wynik[0], poczatek=baza[0], color="g", linestyle="dotted")
rysuj_wektor(wynik[1], poczatek=baza[1], color="g", linestyle="dotted")
plt.axis([-0.5, 4, -0.5, 4])
plt.show()

try:
  eigenvalues, eigenvectors = LA.eig(PHI)

  print("Wartości własne:")
  print(eigenvalues)
  print("Wektory własne:")
  print(eigenvectors)


except LA.LinAlgError:
  print("Nie udało się wyliczyć wartości i wektorów własnych")

[[2 1]
 [1 2]]

Wartości własne:
[3. 1.]
Wektory własne:
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

Pakiet ten umożliwia też między innymi rozwiązywanie układu równań typu \(Ax=B\)

służy do tego funkcja

numpy.linalg.solve(A,B)

która wylicza dokładną wartość x równania macierzy pełnego rzędu.

A musi być macierzą kwadratową, pełnego rzędu, wszystkie wiersze muszą być od siebie liniowo niezależne.

Jeżeli warunek ten jest nie spełniony należy skorzystać z

numpy.linalg.lstsq(A,B)

metodę najmniejszych kwadratów do aproksymacji wyniku równania

Przykładowe zadanie

Rozwiązać układ równań

\[2x_1 +5x_2 +4x_3 = 2 \\ x_1 +3x_2 +2x_3 = 1 \\ 2x_1 +5x_2 +2x_3 = 3\]

A = np.array([[2,5,4],[1,3,2],[2, 5, 2]])
B = np.transpose(np.array([[2,1,3]]))

LA.solve(A,B)

array([[ 2. ],
       [ 0. ],
       [-0.5]])

Praca domowa

Celem pracy domowej będzie zaprojektowanie filtra stosowanego w wielu programach graficznych (np. Photoshop). Pozwala on na przejście z jednego obrazu do drugiego. By to osiągnąć trzeba dla każdego pixela obrazu A sprawdzić czy jego wartość jest mniejsza niż 0.5 a następnie zastosować poniższy wzór.

Overlay blending mode formula: \(\begin{equation} f(a,b) = \begin{cases} 2ab & \text{gdy a < 0.5}\\ 1 - 2(1-a)(1-b) & \text{w przeciwnym przypadku}\\ \end{cases} \end{equation}\)

gdzie:

a - to pojedynczy pixel obrazu A znormalizowany do przedziału 0-1

b - to pojedynczy pixel obrazu B znormalizowany do przedziału 0-1

Do rozwiązania tego zadania została wykorzystana biblioteka OpenCV, o której więcej powiem następnym razem.

Ważne by oba zdjęcia miały takie same wymiary!!!

Zdjęcia w OpenCV przechowywane są w następujących wymiarach.

(wysokość, szerokość, 3)

3 wynika z faktu iż obraz kolorowy składa się z trzech kanałów (RGB - red, green, blue)

Powyższy wzór trzeba zastosować dla każdego kanału!

Powyższy wzór trzeba zastosować dla znormalizowanego obrazu (zmienne norm_image i norm_filter)

Celem pracy domowej nie jest napisanie rozwiązania optymalnego, iterowanie po całym obiekcie zdjęcia jest dopuszczalne.

import cv2
import matplotlib.pyplot as plt
import numpy as np

# poniższe linie nie są potrzebe jeżeli nie korzystacie z google colab
from google.colab import drive
from google.colab.patches import cv2_imshow
drive.mount('/content/drive')


# obraz który będzie wykorzystywany jako filtr
# imread potrzebuje ścieżkę do pliku, jeżeli jest w tym samym folderze 
#co skrypt to po prostu 'nazwa_pliku.rozszerzenie'
filter_img = cv2.imread('/content/drive/My Drive/Warsztaty/filter.jpg')


# domyślnie cv2 otwiera obrazy w trybie BGR, zmieniamy to na RGB
filter_img = cv2.cvtColor(filter_img, cv2.COLOR_BGR2RGB)
# (opcjonalne) wyświetlenie zdjęcia
# plt.imshow(filter_img)
# plt.show()

# obraz na który będziemy nakładać filtr
img = cv2.imread('/content/drive/My Drive/Warsztaty/foreground.png')
# domyślnie cv2 otwiera obrazy w trybie BGR, zmieniamy to na RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# (opcjonalne) wyświetlenie zdjęcia
# plt.imshow(img)
# plt.show()

# normalizacja obrazu
norm_image = cv2.normalize(img, None, alpha=0, beta=1, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_32F)
# (opcjonalne) wyświetlenie zdjęcia znormalizowanego
# plt.imshow(norm_image)
# plt.show()

# normalizacja obrazu
norm_filter = cv2.normalize(filter_img, None, alpha=0, beta=1, norm_type=cv2.NORM_MINMAX, dtype=cv2.CV_32F)
# (opcjonalne) wyświetlenie zdjęcia znormalizowanego
# plt.imshow(norm_filter)
# plt.show()


# pobranie wysokości i szerokości zdjęć (oba powinny być takich samych rozmiarów)
height = norm_image.shape[0]
width = norm_image.shape[1]

#utwórz tablicę o wymiarach (wysokość, szerokość), 
#która przechowuje 3 obiekty typu float

# miejsce na twój kod

#przeiteruj po wszystkich pixelach zdjęć (podwójna pętla, raz po wysokości, raz po szerokości) i zastosuj wzór,
#wynik wzoru przypisz do odpowiedniej komórki zdefiniowanej tablicy

# miejsce na twój kod

# wyświetl utworzoną przez ciebie tablicę, 
# u mnie nazywa się ona mod_img

plt.imshow(mod_img)
plt.show()

Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).

---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

<ipython-input-104-e2eb292735ca> in <module>()
     59 # u mnie nazywa się ona mod_img
     60 
---> 61 plt.imshow(mod_img)
     62 plt.show()

NameError: name 'mod_img' is not defined

Co dalej?

Na następnych zajęciach zaczniemy pracę z rzeczywistymi danymi, rozszerzymy naszą wiedzę o bibliotece Matplotlib i wiele więcej!

Poniżej przykładów kilka kodów, które napisałem w 2-3 semestrze na potrzeby różnych przedmiotów. Po następnych zajęciach, napisanie tego typu kodu nie powinno stanowić dla ciebie większego problemu :)

#ZADANIE2
#Napiecie wyjsciowe Vce
Vce=np.array([0, 0.5, 1, 2, 3, 4, 5, 6, 7, 8])
#Prad wyjściowy Ic(mA) przy stałej wartości prądu wejściowego
Ib0=np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
Ib10=np.array([0, 1.07, 2.43, 2.61, 3.41, 8.13, 2.95, 3.11, 4.22, 3.61])
Ib20=np.array([0.01, 1.15, 5.32, 6.11, 6.27, 6.14, 6.17, 6.98, 6.12, 5.87])
Ib30=np.array([0.01, 1.19, 8.28, 9.47, 9.55, 9.75, 8.57, 7.08, 6.53, 6.57])
Ib40=np.array([0.02, 1.21, 12.20, 12.26, 12.03, 12.82, 12.20, 7.24, 8.12, 8.86])
z1=np.polyfit(Vce,Ib0,2)
z2=np.polyfit(Vce,Ib10,5)
z3=np.polyfit(Vce,Ib20,6)
z4=np.polyfit(Vce,Ib30,5)
z5=np.polyfit(Vce,Ib40,6)
p_1=np.poly1d(z1)
p_2=np.poly1d(z2)
p_3=np.poly1d(z3)
p_4=np.poly1d(z4)
p_5=np.poly1d(z5)
xp=np.linspace(start=0.1,stop=7.8, num=100)
p1 = plt.plot(Vce,Ib0,color="blue",linestyle='-',marker="o", alpha=0.5,label="Wartości odnotowane Ib = 0"+u'\u03bc'+"A")
p11 = plt.plot(xp,p_1(xp),'b:',alpha=0.3)
p2 = plt.plot(Vce,Ib10,color="aqua",linestyle='-',marker="v",alpha=0.5,label="Wartości odnotowane Ib = 10"+u'\u03bc'+"A")
p22 = plt.plot(xp,p_2(xp),'b:',alpha=0.3)
p3 = plt.plot(Vce,Ib20,color="aquamarine",linestyle='-',marker="s", alpha=0.5,label="Wartości odnotowane Ib = 20"+u'\u03bc'+"A")
p33 = plt.plot(xp,p_3(xp),'b:',alpha=0.3)
p4 = plt.plot(Vce,Ib30,color="teal",linestyle='-',marker="p", alpha=0.5,label="Wartości odnotowane Ib = 30"+u'\u03bc'+"A")
p44 = plt.plot(xp,p_4(xp),'b:',alpha=0.3)
p5 = plt.plot(Vce,Ib40,color="cyan",linestyle='-',marker="x", alpha=0.5,label="Wartości odnotowane Ib = 40"+u'\u03bc'+"A")
p55 = plt.plot(xp,p_5(xp),'b:',alpha=0.3,label="Krzywe dopasowania")
plt.subplots_adjust(wspace=20)
plt.legend(loc='upper right')
plt.xlabel("Napięcie wejściowe Vce[V]")
plt.ylabel("Prąd wyjściowy Ic[mA] gdy Ib=const")
plt.show()

import random
import numpy as np
import statistics as st
import matplotlib.pyplot as plt

data = []
miejsce = [] #0 - wies 1 - miasto
dochod = []
czas_pracy = []
for i in range(100):
    if i<=49: miejsce.append(1)
    else: miejsce.append(0)
    if miejsce[-1]==0:
        dochod.append(random.randrange(1500,3000))
    else:
        dochod.append(random.randrange(1800,4000))
    if dochod[-1] in range(1500,2200):
        czas_pracy.append(random.randrange(6,9))
    else:
        czas_pracy.append(random.randrange(8,11))
data = [(miejsce[i], dochod[i], czas_pracy[i]) for i in range(100)]

min_dochod = min(dochod)
max_dochod = max(dochod)
min_czas_pracy = min(czas_pracy)
max_czas_pracy = max(czas_pracy)
range_dochod = max_dochod - min_dochod
range_czas_pracy = max_czas_pracy - min_czas_pracy
mean_dochod = round(np.mean(dochod),2)
mean_czas_pracy = round(np.mean(czas_pracy),2)
median_dochod = st.median(dochod)
median_czas = st.median(czas_pracy)

print("\nTotal:\n")
print(
    "\tMinimalny dochod: ",min_dochod, "\t\t\t\tMaksymalny dochod:",max_dochod,"\n",
"\tMinimalny czas pracy: ",min_czas_pracy,"\t\t\t\tMaksymalny czas pracy: ",max_czas_pracy,"\n",
    "\tRozstep dochodow: ",range_dochod,"\t\t\t\tRozstep czasu: ", range_czas_pracy,"\n",
    "\tSredni dochod: ",mean_dochod, "\t\t\t\tSredni czas pracy: ", mean_czas_pracy,'\n',
    "\tMediana dochodu: ",median_dochod, "\t\t\t\tMediana czasu: ",median_czas)
mode_dochod=-1
mode_czas=-1
try:
    mode_dochod = st.mode(dochod)
    mode_czas = st.mode(czas_pracy)
except st.StatisticsError:
    print ("\nNo unique mode found\n")
variance_dochod = round(st.variance(dochod),2)
variance_czas = round(st.variance(czas_pracy),2)
stdev_dochod = round(st.stdev(dochod),2)
stdev_czas = round(st.stdev(czas_pracy),2)
q1_dochod = np.percentile(dochod,25)
q1_czas = np.percentile(czas_pracy,25)
q3_dochod = np.percentile(dochod,75)
q3_czas = np.percentile(czas_pracy,75)
iqr_dochod = q3_dochod-q1_dochod
iqr_czas = q3_czas-q1_czas
print(
    "\tModa dochodu: ", mode_dochod,"\t\t\t\tModa czasu: ",mode_czas,"\n",
    "\tWariancja dochodu: ", variance_dochod,"\t\t\t\tWariancja czasu: ",variance_czas,"\n",
    "\tOdchylenie dochodu: ",stdev_dochod,"\t\t\t\tOdchylenie czasu: ",stdev_czas,"\n",
    "\tKwartyl dolny dochodu: ",q1_dochod,"\t\t\t\tKwartyl dolny czasu: ",q1_czas,"\n",
    "\tKwartyl gorny dochodu: ",q3_dochod,"\t\t\t\tKwartyl gorny czasu: ",q3_czas,"\n"
    "\r Roz kwartylowy dochodu: ",iqr_dochod,"\t\t\t\tRoz kwartylowy czasu: ",iqr_czas,"\n"
)



min_dochod = min(dochod[50:])
max_dochod = max(dochod[50:])
min_czas_pracy = min(czas_pracy[50:])
max_czas_pracy = max(czas_pracy[50:])
range_dochod = max_dochod - min_dochod
range_czas_pracy = max_czas_pracy - min_czas_pracy
mean_dochod = round(np.mean(dochod[50:]),2)
mean_czas_pracy = round(np.mean(czas_pracy[50:]),2)
median_dochod = st.median(dochod[50:])
median_czas = st.median(czas_pracy[50:])

print("\nWies:\n")
print(
    "\tMinimalny dochod: ",min_dochod, "\t\t\t\tMaksymalny dochod:",max_dochod,"\n",
"\tMinimalny czas pracy: ",min_czas_pracy,"\t\t\t\tMaksymalny czas pracy: ",max_czas_pracy,"\n",
    "\tRozstep dochodow: ",range_dochod,"\t\t\t\tRozstep czasu: ", range_czas_pracy,"\n",
    "\tSredni dochod: ",mean_dochod, "\t\t\t\tSredni czas pracy: ", mean_czas_pracy,'\n',
    "\tMediana dochodu: ",median_dochod, "\t\t\t\tMediana czasu: ",median_czas)
mode_dochod=-1
mode_czas=-1
try:
    mode_dochod = st.mode(dochod[50:])
    mode_czas = st.mode(czas_pracy[50:])
except st.StatisticsError:
    print ("\nNo unique mode found\n")
variance_dochod = round(st.variance(dochod[50:]),2)
variance_czas = round(st.variance(czas_pracy[50:]),2)
stdev_dochod = round(st.stdev(dochod[50:]),2)
stdev_czas = round(st.stdev(czas_pracy[50:]),2)
q1_dochod = np.percentile(dochod[50:],25)
q1_czas = np.percentile(czas_pracy[50:],25)
q3_dochod = np.percentile(dochod[50:],75)
q3_czas = np.percentile(czas_pracy[50:],75)
iqr_dochod = q3_dochod-q1_dochod
iqr_czas = q3_czas-q1_czas
print(
    "\tModa dochodu: ", mode_dochod,"\t\t\t\tModa czasu: ",mode_czas,"\n",
    "\tWariancja dochodu: ", variance_dochod,"\t\t\t\tWariancja czasu: ",variance_czas,"\n",
    "\tOdchylenie dochodu: ",stdev_dochod,"\t\t\t\tOdchylenie czasu: ",stdev_czas,"\n",
    "\tKwartyl dolny dochodu: ",q1_dochod,"\t\t\t\tKwartyl dolny czasu: ",q1_czas,"\n",
    "\tKwartyl gorny dochodu: ",q3_dochod,"\t\t\t\tKwartyl gorny czasu: ",q3_czas,"\n"
    "\r Roz kwartylowy dochodu: ",iqr_dochod,"\t\t\t\tRoz kwartylowy czasu: ",iqr_czas,"\n"
)



min_dochod = min(dochod[:50])
max_dochod = max(dochod[:50])
min_czas_pracy = min(czas_pracy[:50])
max_czas_pracy = max(czas_pracy[:50])
range_dochod = max_dochod - min_dochod
range_czas_pracy = max_czas_pracy - min_czas_pracy
mean_dochod = round(np.mean(dochod[:50]),2)
mean_czas_pracy = round(np.mean(czas_pracy[:50]),2)
median_dochod = st.median(dochod[:50])
median_czas = st.median(czas_pracy[:50])

print("\nMiasto:\n")
print(
    "\tMinimalny dochod: ",min_dochod, "\t\t\t\tMaksymalny dochod:",max_dochod,"\n",
"\tMinimalny czas pracy: ",min_czas_pracy,"\t\t\t\tMaksymalny czas pracy: ",max_czas_pracy,"\n",
    "\tRozstep dochodow: ",range_dochod,"\t\t\t\tRozstep czasu: ", range_czas_pracy,"\n",
    "\tSredni dochod: ",mean_dochod, "\t\t\t\tSredni czas pracy: ", mean_czas_pracy,'\n',
    "\tMediana dochodu: ",median_dochod, "\t\t\t\tMediana czasu: ",median_czas)
mode_dochod=-1
mode_czas=-1
try:
    mode_dochod = st.mode(dochod[:50])
    mode_czas = st.mode(czas_pracy[:50])
except st.StatisticsError:
    print ("No unique mode found")
variance_dochod = round(st.variance(dochod[:50]),2)
variance_czas = round(st.variance(czas_pracy[:50]),2)
stdev_dochod = round(st.stdev(dochod[:50]),2)
stdev_czas = round(st.stdev(czas_pracy[:50]),2)
q1_dochod = np.percentile(dochod[:50],25)
q1_czas = np.percentile(czas_pracy[:50],25)
q3_dochod = np.percentile(dochod[:50],75)
q3_czas = np.percentile(czas_pracy[:50],75)
iqr_dochod = q3_dochod-q1_dochod
iqr_czas = q3_czas-q1_czas
print(
    "\tModa dochodu: ", mode_dochod,"\t\t\t\tModa czasu: ",mode_czas,"\n",
    "\tWariancja dochodu: ", variance_dochod,"\t\t\t\tWariancja czasu: ",variance_czas,"\n",
    "\tOdchylenie dochodu: ",stdev_dochod,"\t\t\t\tOdchylenie czasu: ",stdev_czas,"\n",
    "\tKwartyl dolny dochodu: ",q1_dochod,"\t\t\t\tKwartyl dolny czasu: ",q1_czas,"\n",
    "\tKwartyl gorny dochodu: ",q3_dochod,"\t\t\t\tKwartyl gorny czasu: ",q3_czas,"\n"
    "\r Roz kwartylowy dochodu: ",iqr_dochod,"\t\t\t\tRoz kwartylowy czasu: ",iqr_czas,"\n"
)
f = open('dane.txt','w')
for i in range(100):
    line = str(miejsce[i])+","+str(dochod[i])+","+str(czas_pracy[i])+"\n"
    f.writelines(line)
f.close()
bx1_dochod = [dochod[:50]]
plt.boxplot(bx1_dochod)
#"1 dochody w mieście"
plt.title("Boxplot dochodow w miescie")
plt.show()

bx2_dochod = [dochod[50:]]
plt.boxplot(bx2_dochod)
#"1 dochody na wsi"
plt.title("Boxplot dochodow na wsi")
plt.show()

bx_dochod = [dochod[:50], dochod[50:]]
plt.boxplot(bx_dochod)
#"1 - dochody wszystkich 2 - dochody w mieście 3 - dochody na wsi"
plt.title("Boxplot dochodow na wsi i w miescie")
plt.legend()
plt.show()

bx3_dochod = [dochod]
plt.boxplot(bx3_dochod)
#"1 - dochody wszystkich 2 - dochody w mieście 3 - dochody na wsi"
plt.title("Boxplot dochodow (w sumie)")
plt.legend()
plt.show()

##########################################################

bins_edges=[1500,1750,2000,2250,2500,2750,3000,3250,3500,3750,4000]
h1_dochod = [dochod[:50]]
plt.hist(h1_dochod,bins=bins_edges)
plt.ylabel("Liczba osób")
plt.xlabel("Dochody (zł)")
plt.title("Histogram dochodow w miescie")
plt.show()

h2_dochod = [dochod[50:]]
plt.hist(h2_dochod,bins=bins_edges)
plt.ylabel("Liczba osób")
plt.xlabel("Dochody (zł)")
plt.title("Histogram dochodow na wsi")
plt.show()

h_dochod = [dochod[:50], dochod[50:]]
plt.hist(h_dochod,bins=bins_edges)
plt.ylabel("Liczba osób")
plt.xlabel("Dochody (zł)")
plt.title("Histogram dochodow na wsi i w miescie")
plt.show()

h3_dochod = [dochod]
plt.hist(h3_dochod,bins=bins_edges)
plt.ylabel("Liczba osób")
plt.xlabel("Dochody (zł)")
plt.title("Histogram dochodow (w sumie)")
plt.show()

##########################################################

bx1_czas=[czas_pracy[:50]]
plt.title("Boxplot czasu pracy w miescie")
plt.boxplot(bx1_czas)
plt.show()


bx2_czas=[czas_pracy[50:]]
plt.title("Boxplot czasu pracy na wsi")
plt.boxplot(bx2_czas)
plt.show()

bx_czas=[czas_pracy[:50], czas_pracy[50:]]
plt.title("Boxplot czasu pracy na wsi i w miescie")
plt.boxplot(bx_czas)
plt.show()

bx3_czas=[czas_pracy]
plt.title("Boxplot czasu pracy (w sumie)")
plt.boxplot(bx3_czas)
plt.show()

##########################################################

h1_czas = [czas_pracy[:50]]
bins_edges=[6,7,8,9,10,11]
plt.hist(h1_czas,bins=bins_edges,range=[6,11], density=False)
plt.ylabel("Liczba osób")
plt.xlabel("Czas pracy (h)")
plt.title("Histogram czasu pracy w miescie")
plt.show()

h2_czas = [czas_pracy[50:]]
bins_edges=[6,7,8,9,10,11]
plt.hist(h2_czas,bins=bins_edges,range=[6,11], density=False)
plt.ylabel("Liczba osób")
plt.xlabel("Czas pracy (h)")
plt.title("Histogram czasu pracy na wsi")
plt.show()

h_czas = [czas_pracy[:50], czas_pracy[50:]]
bins_edges=[6,7,8,9,10,11]
plt.hist(h_czas,bins=bins_edges,range=[6,11], density=False)
plt.ylabel("Liczba osób")
plt.xlabel("Czas pracy (h)")
plt.title("Histogram czasu pracy na wsi i w miescie")
plt.show()


h3_czas = [czas_pracy]
bins_edges=[6,7,8,9,10,11]
plt.hist(h3_czas,bins=bins_edges,range=[6,11], density=False)
plt.ylabel("Liczba osób")
plt.xlabel("Czas pracy (h)")
plt.title("Histogram czasu pracy (w sumie)")
plt.show()

import matplotlib.pyplot as plt
import numpy as np

# funkcje wykorzystane w zadaniu

def y1(N):
    n = np.arange(0,N)
    phase = np.pi/4
    y = np.cos(2 * np.pi * n/N +phase)
    return y


def y2(N):
    n = np.arange(0,N)
    phase = 0
    y = 0.5 * np.cos(4 * np.pi*n/N + phase)
    return y


def y3(N):
    n = np.arange(0,N)
    phase = np.pi / 2
    y = 0.25 * np.cos( 8 * np.pi*n/N + phase)
    return y


def y4(y1, y2, y3):
    a = y1 + y2 + y3
    return a


if __name__ == "__main__":
    N = 32  # zmienna okreslająca ilość próbek

    # Wygenerowanie funkcji
    func1 = y1(N)
    func2 = y2(N)
    func3 = y3(N)
    func4 = y4(func1, func2, func3)

    # Część rzeczywista funkcji sinusoidalnych
    plt.figure().suptitle("Część rzeczywista funkcji sinusoidalnych")
    plt.subplot(2, 2, 1)
    plt.plot(func1)
    plt.xlabel("Nr próbki")
    plt.ylabel("Amplituda")
    plt.title(r'$y_1=\cos$(2$\pi \cdot \frac{n}{N}$+$\frac{\pi}{4}$)')
    plt.subplot(2, 2, 2)
    plt.plot(func2)
    plt.xlabel("Nr próbki")
    plt.ylabel("Amplituda")
    plt.title(r'$y_2=\frac{1}{2}\cos$(4$\pi \cdot \frac{n}{N}$)')
    plt.subplot(2, 2, 3)
    plt.plot(func3)
    plt.xlabel("Nr próbki")
    plt.ylabel("Amplituda")
    plt.title(r'$y_3=\frac{1}{4}\cos$(8$\pi \cdot \frac{n}{N}$ +$\frac{\pi}{2}$)')
    plt.subplot(2, 2, 4)
    plt.title(r'$y_4$ = $y_1+y_2+y_3$')
    plt.plot(func4)
    plt.xlabel("Nr próbki")
    plt.ylabel("Amplituda")
    plt.tight_layout()
    plt.show()
    

    # Wyliczenia transformat Fouriera oraz innych parametrów dla każdej funkcji
    fourier1 = 2*np.fft.fft(func1)/N
    real1 = fourier1.real
    imaginary1 = fourier1.imag
    angle1 = np.angle(fourier1)
    modulus1 = np.abs(fourier1)

    fourier2 = 2*np.fft.fft(func2)/N
    real2 = fourier2.real
    imaginary2 = fourier2.imag
    angle2 = np.angle(fourier2)
    modulus2 = np.abs(fourier2)

    fourier3 = 2*np.fft.fft(func3)/N
    real3 = fourier3.real
    imaginary3 = fourier3.imag
    angle3 = np.angle(fourier3)
    modulus3 = np.abs(fourier3)

    fourier4 = 2*np.fft.fft(func4)/N
    real4 = fourier4.real
    imaginary4 = fourier4.imag
    angle4 = np.angle(fourier4)
    modulus4 = np.abs(fourier4)


    # Transformata Fouriera cz. rzeczywista
    plt.figure().suptitle("Część rzeczywista Transformaty Fouriera")
    plt.subplot(2, 2, 1)
    plt.ylim(-0.05, 0.8)
    plt.stem(real1, use_line_collection=True)
    plt.hlines(np.abs(round(real1[1], 3)), 0, 32, colors="red", linestyles="dotted")
    plt.yticks((0,0.25,0.5, np.abs(round(imaginary1[1], 3))))
    plt.xlabel("Nr pasma częstotliwościowego")
    plt.ylabel("Amplituda")
    plt.title(r'$y_1=\cos$(2$\pi \cdot \frac{n}{N}$+$\frac{\pi}{4}$)')
    plt.subplot(2, 2, 2)
    plt.ylim(-0.05, 0.8)
    plt.yticks((0,0.250, np.abs(round(real2[2], 3)),0.707))
    plt.stem(real2, use_line_collection=True)
    plt.hlines(np.abs(round(real2[2], 3)), 0, 32, colors="orange", linestyles="dotted")
    plt.xlabel("Nr pasma częstotliwościowego")
    plt.ylabel("Amplituda")
    plt.title(r'$y_2=\frac{1}{2}\cos$(4$\pi \cdot \frac{n}{N}$)')
    plt.subplot(2, 2, 3)
    plt.ylim(-0.05, 0.8)
    plt.yticks((np.abs(round(real3[4], 3)),0.250,0.50,0.707))
    plt.stem(real3, use_line_collection=True)
    plt.hlines(np.abs(round(real3[4], 3)), 0, 32, colors="gold", linestyles="dotted")
    plt.xlabel("Nr pasma częstotliwościowego")
    plt.ylabel("Amplituda")
    plt.title(r'$y_3=\frac{1}{4}\cos$(8$\pi \cdot \frac{n}{N}$ +$\frac{\pi}{2}$)')
    plt.subplot(2, 2, 4)
    plt.ylim(-0.05, 0.8)
    plt.yticks((np.abs(round(real3[4], 3)), 0.25, np.abs(round(real2[2], 3)),np.abs(round(real1[1], 3)) ))
    plt.hlines(np.abs(round(real1[1], 3)), 0, 32, colors="red", linestyles="dotted")
    plt.hlines(np.abs(round(real2[2], 3)), 0, 32, colors="orange", linestyles="dotted")
    plt.hlines(np.abs(round(real3[4], 3)), 0, 32, colors="gold", linestyles="dotted")
    plt.title(r'$y_4$ = $y_1+y_2+y_3$')
    plt.stem(real4, use_line_collection=True)
    plt.xlabel("Nr pasma częstotliwościowego")
    plt.ylabel("Amplituda")
    plt.tight_layout()
    plt.show()