Introduction to Data Analysis with Python
PART 2 Matplotlib
Podstawy analizy danych
1. Matplotlib
- Podstawowe informacje
- Plot
- Scatter + Stem + subplots
- Boxplots - wykresy pudełkowe
- Barplots - wykresy kolumnowe
- Pieplots- wykresy kołowe
- Polar - wykresy liczb urojonych
- Obsługa obrazów - PIL
1. Podstawowe informacje
Matplotlib jest to podstawowa biblioteka do generowania wykresów graficznych i wizualizacji danych w Pythonie.
Przydatne linki:
- https://matplotlib.org/
- https://matplotlib.org/tutorials/
- https://matplotlib.org/tutorials/introductory/pyplot.html
- https://matplotlib.org/3.1.1/tutorials/index.html
- https://towardsdatascience.com
- gotowe kody różnych wykresów
Dodatkowe biblioteki bazujące lub podobne do matplotlib:
Seaborn - biblioteka oparta na matplotlib stworzona konkretnie do wizualizacji danych statystycznych, posiada dobrą współpracę z biblioteką pandas. Gdzie matplotlib nie może, tam seaborn pośle.
Plotly - biblioteka do tworzenia pięknych i interaktywnych wykresów z wykorzystaniem biblioteki/frameworku Dash. Istnieje wersja płatna , lecz rozwiązanie w wersji darmowej oferuje sporą część swojej rozległej funkcjonalności.
2. Plot
Spróbujmy wygenerować nasz pierwszy wykres. W tym celu należy pobrać bibliotekę
import matplotlib.pyplot as plt
podać oś X, oś Y i poleceniem
plt.plot(oś X, oś Y)
wygenerować wykres
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.plot(x,y)
plt.show() # bez tej komendy w jupiter notebook wyświetli nam wykres, ale w normalnych warunkach ta komenda jest niezbędna
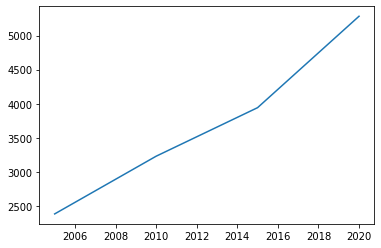
Mamy nasz wykres, ale co oznaczają konkretne dane? Podpiszmy wykres oraz osie. Służą do tego polecenia
plt.xlabel("Opis osi X")
plt.ylabel("Opis osi Y")
plt.title("Opis wykresu")
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.plot(x,y)
plt.title("Przeciętne zarobki w Polsce w sektorze przedsiębiorstw - Polska")
plt.xlabel("Rok")
plt.ylabel("Wynagrodznie (zł)")
Text(0, 0.5, 'Wynagrodznie (zł)')
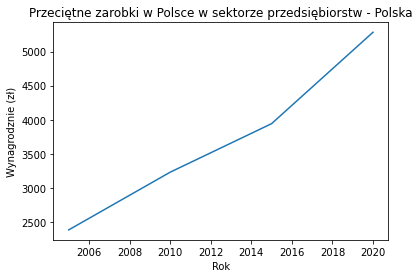
Jest już trochę lepiej, ale jak popatrzymy na nasze dane, to mamy informacje z konkretnych lat, zaś biblioteka sobie automatycznie dopasowała krok w osiach. Jeżeli chcemy sami ustawić dla osi X:
plt.xticks(ticks=None, labels=None)
Dla osi Y:
plt.yticks(ticks=None, labels=None)
gdzie:
- ticks - lista wartości, które chcemy wyświetlać
- label - lista o takim samym rozmiarze co ticks, która precyzuje co ma być wyświetlane, jeżeli istnieje jakiś alternatywny zapis, nie jest obowiązkowa
Przykład:
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0, 2*np.pi, 0.1)
y = np.sin(x)
plt.plot(x,y)
plt.title("y = sin(x)")
plt.show()
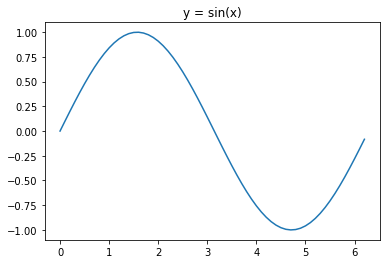
Po zastosowaniu formatowania tekstu na osiach
import matplotlib.pyplot as plt
from math import sqrt
x = np.arange(0, 2*np.pi, 0.1)
y = np.sin(x)
plt.plot(x,y)
plt.title("y = sin(x)")
plt.xticks([0,np.pi/6, np.pi/4, np.pi/3, np.pi/2, np.pi, 3*np.pi/2, 2*np.pi], ['0', r'$\frac{\pi}{6}$',r'$\frac{\pi}{4}$', r'$\frac{\pi}{3}$', r'$\frac{\pi}{2}$', r'$\pi$', r'$\frac{3\pi}{2}$', r'$2\pi$' ] )
plt.yticks([0,0.5, sqrt(2)/2, sqrt(3)/2, 1],['0',r'$\frac{1}{2}$', r'$\frac{\sqrt{2}}{2}$', r'$\frac{\sqrt{3}}{2}$', '1'])
plt.show()
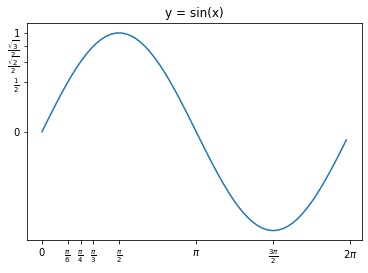
Wracając do przykładu z wynagrodzeniem
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.plot(x,y)
plt.title("Przeciętne zarobki w Polsce w sektorze przedsiębiorstw - Polska")
plt.xlabel("Rok")
plt.ylabel("Wynagrodznie (zł)")
plt.xticks([2005,2010,2015,2020])
plt.yticks([2000,3000,4000,5000])
plt.show()
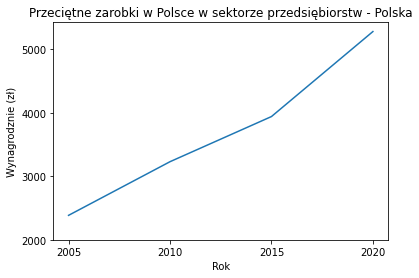
Do ograniczenia zakresu wykresy wykorzystywane są metody
Dla osi X:
plt.xlim(limit_dolny, limit_górny)
Dla osi Y:
plt.ylim(limit_dolny, limit_górny)
Domyślnie biblioteka stara się dopasować zakresy do danych, które jej podamy. Ale nic nie stoi na przeszkodzie byśmy ograniczyli tego do naszych potrzeb.
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.plot(x,y)
plt.title("Przeciętne zarobki w Polsce w sektorze przedsiębiorstw - Polska")
plt.xlabel("Rok")
plt.ylabel("Wynagrodznie (zł)")
plt.xticks([2005,2010,2015,2020])
plt.yticks([2000,3000,4000,5000])
plt.xlim(2010,2020)
plt.ylim(3000, 5000)
plt.show()
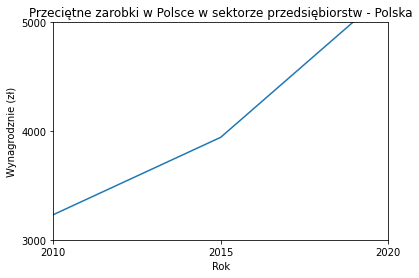
By wykres był lepiej sformatowany można skorzystać z wielu dodatkowych parametrów, które można przekazać do metody plot, takich jak:
| Nazwa parametru | Opis |
|---|---|
| color/c | kolor wykresu |
| alpha | przezroczystość, od 0 do 1 |
| label | opis wykresu do wykorzystania w legendzie |
| marker | definiuje styl punktów charakterystycznych |
| linestyle | styl linii |
i wiele innych
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.title("Przeciętne zarobki w Polsce w sektorze przedsiębiorstw - Polska")
plt.xlabel("Rok")
plt.ylabel("Wynagrodznie (zł)")
plt.xticks([2005,2010,2015,2020])
plt.yticks([2000,3000,4000,5000])
plt.plot(x,y, color="cyan", alpha=0.5, label="Wynagrodzenie", marker="o", linestyle="--")
plt.legend() #polecenie potrzebne by dodać legendę
plt.show()

Jako, że styl linii i kolor podaje się często, istnieje uproszczony zapis
litera koloru, marker, styl linii
np.
import matplotlib.pyplot as plt
x = [2005,2010,2015,2020]
y = [2385.39, 3231.13, 3942.78, 5282.8]
plt.title("Przeciętne zarobki w Polsce w sektorze przedsiębiorstw - Polska")
plt.xlabel("Rok")
plt.ylabel("Wynagrodznie (zł)")
plt.xticks([2005,2010,2015,2020])
plt.yticks([2000,3000,4000,5000])
plt.plot(x,y, "ro:", alpha=0.5, label="Wynagrodzenie")
plt.legend() #polecenie potrzebne by dodać legendę
plt.show()
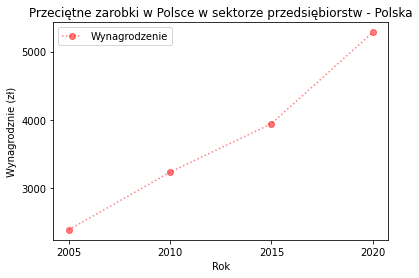
3. Scatter + Stem + subplots
Do dużej liczby danych rozproszonych zamiast metody plot warto skorzystać z metody scatter. Reszta parametrów nie ulega zmianie i jest bardzo podoba do tego co przed chwilą omówiliśmy.
Źródło: https://matplotlib.org/3.3.2/gallery/lines_bars_and_markers/scatter_masked.html
import matplotlib.pyplot as plt
import numpy as np
# Fixing random state for reproducibility
np.random.seed(19680801)
N = 100
r0 = 0.6
x = 0.9 * np.random.rand(N)
y = 0.9 * np.random.rand(N)
area = (20 * np.random.rand(N))**2 # 0 to 10 point radii
c = np.sqrt(area) # kolor zależy od pola
r = np.sqrt(x ** 2 + y ** 2)
area1 = np.ma.masked_where(r < r0, area)
area2 = np.ma.masked_where(r >= r0, area)
plt.scatter(x, y, s=area1, marker='^', c=c)
plt.scatter(x, y, s=area2, marker='o', c=c)
plt.show()

Wykresem który łączy plot ze scatter jest stem.
plt.stem(x,y)
Gdzie:
- x - lista danych z osi X
- y - lista danych z osi Y
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0.1, 2 * np.pi, 41)
y = np.exp(np.sin(x))
plt.stem(x, y, use_line_collection=True)
plt.show()
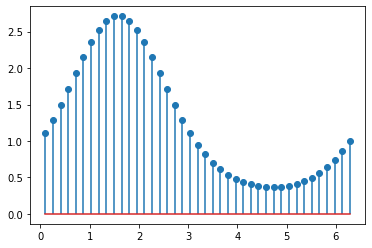
Domyślnie program tworzy jedną figurę (tak nazywany jest poszczególny obraz w matplotlib) i będzie ją nadpisywać tak długo jak długo nie wywołamy metody show. Pozwala nam to zawrzeć kilka wykresów na jednym obrazie.
#ZADANIE2
#Napiecie wyjsciowe Vce
Vce=np.array([0, 0.5, 1, 2, 3, 4, 5, 6, 7, 8])
#Prad wyjściowy Ic(mA) przy stałej wartości prądu wejściowego
Ib20=np.array([0.01, 1.15, 5.32, 6.11, 6.27, 6.14, 6.17, 6.98, 6.12, 5.87])
Ib30=np.array([0.01, 1.19, 8.28, 9.47, 9.55, 9.75, 8.57, 7.08, 6.53, 6.57])
Ib40=np.array([0.02, 1.21, 12.20, 12.26, 12.03, 12.82, 12.20, 7.24, 8.12, 8.86])
z3=np.polyfit(Vce,Ib20,6)
z4=np.polyfit(Vce,Ib30,5)
z5=np.polyfit(Vce,Ib40,6)
p_3=np.poly1d(z3)
p_4=np.poly1d(z4)
p_5=np.poly1d(z5)
xp=np.linspace(start=0.1,stop=7.8, num=100)
p3 = plt.plot(Vce,Ib20,color="aquamarine",linestyle='-',marker="s", alpha=0.5,label="Wartości odnotowane Ib = 20"+u'\u03bc'+"A")
p33 = plt.plot(xp,p_3(xp),'b:',alpha=0.3)
p4 = plt.plot(Vce,Ib30,color="teal",linestyle='-',marker="p", alpha=0.5,label="Wartości odnotowane Ib = 30"+u'\u03bc'+"A")
p44 = plt.plot(xp,p_4(xp),'b:',alpha=0.3)
p5 = plt.plot(Vce,Ib40,color="cyan",linestyle='-',marker="x", alpha=0.5,label="Wartości odnotowane Ib = 40"+u'\u03bc'+"A")
p55 = plt.plot(xp,p_5(xp),'b:',alpha=0.3,label="Krzywe dopasowania")
plt.subplots_adjust(wspace=20)
plt.legend(loc='lower right') #można dokreślić gdzie ma znajdować się legenda
plt.xlabel("Napięcie wejściowe Vce[V]")
plt.ylabel("Prąd wyjściowy Ic[mA] gdy Ib=const")
plt.show()
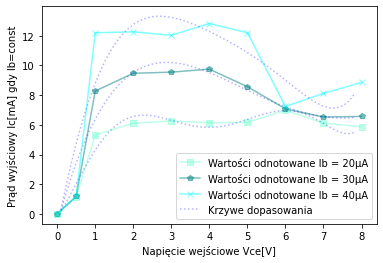
Jeżeli jednak chcemy rozbić nasze obliczenia na kilka różnych obrazów. Musimy zrozumieć koncepcje figur, osi oraz subplotów. Dotychczasowy zapis, który wykorzystywaliśmy jest tak naprawdę uproszczeniem poniższego zapisu.
plt.subplots(nrows=1, ncols=1)
Gdzie:
- nrows - ile szeregów wykresów
- ncols - ile kolumn wykresów
Metoda ta zwraca figurę, oraz osie (lub listę osi) w których będziemy rysować wykresy.
import numpy as np
import matplotlib.pyplot as plt
# First create some toy data:
x = np.linspace(0, 2*np.pi, 400)
y = np.sin(x**2)
# Create just a figure and only one subplot
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_title('Simple plot') #metody wykorzystywane w osiach różnią się nazwą, zamiast plt.title mamy ax.set_title
# Create two subplots and unpack the output array immediately
f, (ax1, ax2) = plt.subplots(1, 2, sharey=True)
ax1.plot(x, y)
ax1.set_title('Sharing Y axis')
ax2.scatter(x, y)
# Create four polar axes and access them through the returned array
fig, axs = plt.subplots(2, 2, subplot_kw=dict(polar=True))
axs[0, 0].plot(x, y)
axs[1, 1].scatter(x, y)
plt.show()
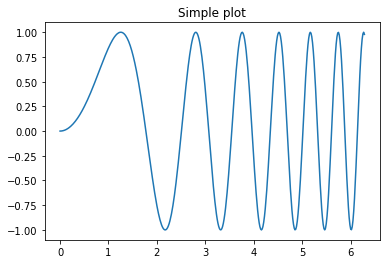
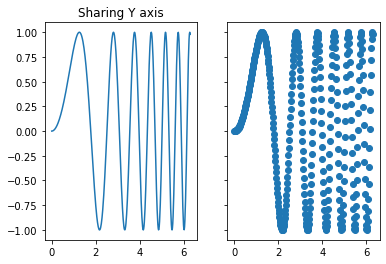
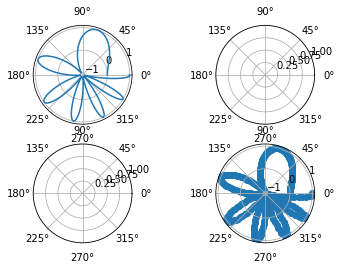
Całkowity obraz składa się z poszczególnych obrazów (figure), które z kolei składają się ze składowych/osi (axes). Na początku, może to nastręczać dużo problemów w rozumieniu. Zapis jest też trochę utrudniony, niektóre metody nazywają się inaczej. Zachęcam do przeczytania wyjaśnienia, np. tutaj:
https://medium.com/towards-artificial-intelligence/day-3-of-matplotlib-figure-axes-explained-in-detail-d6e98f7cd4e7
import matplotlib.pyplot as plt
import numpy as np
# funkcje wykorzystane w zadaniu
def y1(N):
n = np.arange(0,N)
phase = np.pi/4
y = np.cos(2 * np.pi * n/N +phase)
return y
def y2(N):
n = np.arange(0,N)
phase = 0
y = 0.5 * np.cos(4 * np.pi*n/N + phase)
return y
def y3(N):
n = np.arange(0,N)
phase = np.pi / 2
y = 0.25 * np.cos( 8 * np.pi*n/N + phase)
return y
def y4(y1, y2, y3):
a = y1 + y2 + y3
return a
if __name__ == "__main__":
N = 32 # zmienna okreslająca ilość próbek
# Wygenerowanie funkcji
func1 = y1(N)
func2 = y2(N)
func3 = y3(N)
func4 = y4(func1, func2, func3)
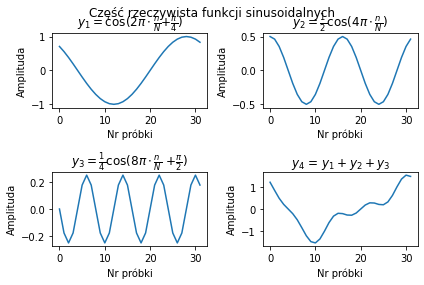
# Część rzeczywista funkcji sinusoidalnych
plt.figure().suptitle("Część rzeczywista funkcji sinusoidalnych")
plt.subplot(2, 2, 1)
plt.plot(func1)
plt.xlabel("Nr próbki")
plt.ylabel("Amplituda")
plt.title(r'$y_1=\cos$(2$\pi \cdot \frac{n}{N}$+$\frac{\pi}{4}$)')
plt.subplot(2, 2, 2)
plt.plot(func2)
plt.xlabel("Nr próbki")
plt.ylabel("Amplituda")
plt.title(r'$y_2=\frac{1}{2}\cos$(4$\pi \cdot \frac{n}{N}$)')
plt.subplot(2, 2, 3)
plt.plot(func3)
plt.xlabel("Nr próbki")
plt.ylabel("Amplituda")
plt.title(r'$y_3=\frac{1}{4}\cos$(8$\pi \cdot \frac{n}{N}$ +$\frac{\pi}{2}$)')
plt.subplot(2, 2, 4)
plt.title(r'$y_4$ = $y_1+y_2+y_3$')
plt.plot(func4)
plt.xlabel("Nr próbki")
plt.ylabel("Amplituda")
plt.tight_layout()
plt.show()
# Wyliczenia transformat Fouriera oraz innych parametrów dla każdej funkcji
fourier1 = 2*np.fft.fft(func1)/N
real1 = fourier1.real
imaginary1 = fourier1.imag
angle1 = np.angle(fourier1)
modulus1 = np.abs(fourier1)
fourier2 = 2*np.fft.fft(func2)/N
real2 = fourier2.real
imaginary2 = fourier2.imag
angle2 = np.angle(fourier2)
modulus2 = np.abs(fourier2)
fourier3 = 2*np.fft.fft(func3)/N
real3 = fourier3.real
imaginary3 = fourier3.imag
angle3 = np.angle(fourier3)
modulus3 = np.abs(fourier3)
fourier4 = 2*np.fft.fft(func4)/N
real4 = fourier4.real
imaginary4 = fourier4.imag
angle4 = np.angle(fourier4)
modulus4 = np.abs(fourier4)
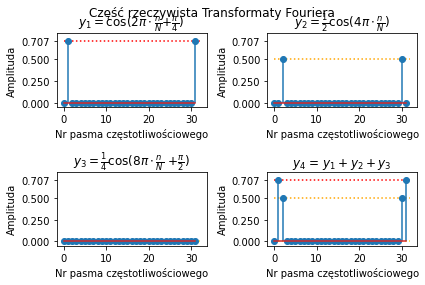
# Transformata Fouriera cz. rzeczywista
plt.figure().suptitle("Część rzeczywista Transformaty Fouriera")
plt.subplot(2, 2, 1)
plt.ylim(-0.05, 0.8)
plt.stem(real1, use_line_collection=True)
plt.hlines(np.abs(round(real1[1], 3)), 0, 32, colors="red", linestyles="dotted")
plt.yticks((0,0.25,0.5, np.abs(round(imaginary1[1], 3))))
plt.xlabel("Nr pasma częstotliwościowego")
plt.ylabel("Amplituda")
plt.title(r'$y_1=\cos$(2$\pi \cdot \frac{n}{N}$+$\frac{\pi}{4}$)')
plt.subplot(2, 2, 2)
plt.ylim(-0.05, 0.8)
plt.yticks((0,0.250, np.abs(round(real2[2], 3)),0.707))
plt.stem(real2, use_line_collection=True)
plt.hlines(np.abs(round(real2[2], 3)), 0, 32, colors="orange", linestyles="dotted")
plt.xlabel("Nr pasma częstotliwościowego")
plt.ylabel("Amplituda")
plt.title(r'$y_2=\frac{1}{2}\cos$(4$\pi \cdot \frac{n}{N}$)')
plt.subplot(2, 2, 3)
plt.ylim(-0.05, 0.8)
plt.yticks((np.abs(round(real3[4], 3)),0.250,0.50,0.707))
plt.stem(real3, use_line_collection=True)
plt.hlines(np.abs(round(real3[4], 3)), 0, 32, colors="gold", linestyles="dotted")
plt.xlabel("Nr pasma częstotliwościowego")
plt.ylabel("Amplituda")
plt.title(r'$y_3=\frac{1}{4}\cos$(8$\pi \cdot \frac{n}{N}$ +$\frac{\pi}{2}$)')
plt.subplot(2, 2, 4)
plt.ylim(-0.05, 0.8)
plt.yticks((np.abs(round(real3[4], 3)), 0.25, np.abs(round(real2[2], 3)),np.abs(round(real1[1], 3)) ))
plt.hlines(np.abs(round(real1[1], 3)), 0, 32, colors="red", linestyles="dotted")
plt.hlines(np.abs(round(real2[2], 3)), 0, 32, colors="orange", linestyles="dotted")
plt.hlines(np.abs(round(real3[4], 3)), 0, 32, colors="gold", linestyles="dotted")
plt.title(r'$y_4$ = $y_1+y_2+y_3$')
plt.stem(real4, use_line_collection=True)
plt.xlabel("Nr pasma częstotliwościowego")
plt.ylabel("Amplituda")
plt.tight_layout()
plt.show()
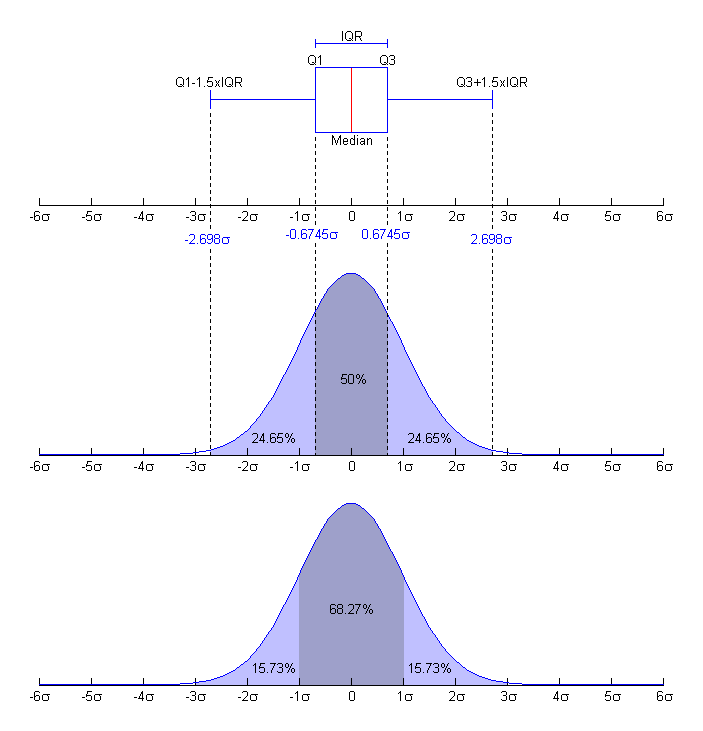
4. Boxplots - wykresy pudełkowe
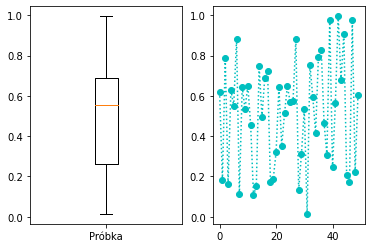
Do danych giełdowych bardzo często wykorzystywane są tak zwane wykresy pudełkowe, świecowe. Zakres pudełka oznacza pierwszy (dolny) i trzeci (górny) kwartyl, które odpowiednio oznaczają, że 25% i 75% danych znajduje się poniżej tych wartości. Linią przecinającą pudło oznacza się gdzie występuje mediana wartości. Zaś wąsami pudła oznacza się maksymalne odchylenia wartości (minimum i maksimum), z ograniczeniem rozmiaru wąsów dla ich czytelności.
import numpy as np
import matplotlib.pyplot as plt
data = np.random.rand(50)
fig, ax = plt.subplots(1,2)
ax[0].boxplot(data, labels=["Próbka"])
ax[1].plot(data, "co:")
plt.show()
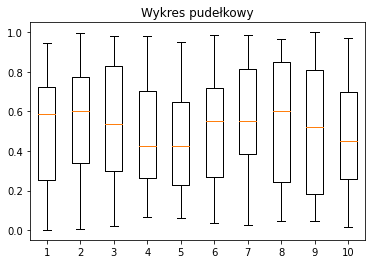
import numpy as np
import matplotlib.pyplot as plt
data = np.random.rand(50,10) # wygenerowanie 10 serii po 50 wartości z przedziału 0 - 1
plt.boxplot(data)
plt.title("Wykres pudełkowy")
plt.show()
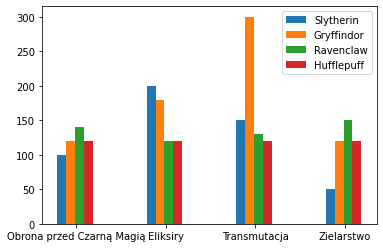
5. Barplots - wykresy kolumnowe
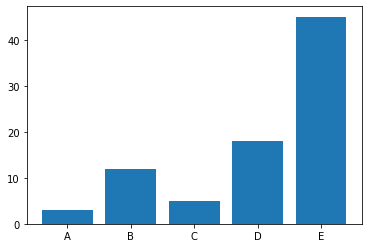
Kolejnym wykresem są bardzo popularne wykresy kolumnowe, wykorzystywane do porównania danych dyskretnych. Każdy słupek w wykresie ma odpowiednią wysokość, która koresponduje proporcjonalnie do wartości danej zmiennej.
plt.bar(x, height, width=0.8)
Gdzie:
- x - sekwencja koordynatów wykresu kolumnowego
- height - sekwencja wysokości poszczególnych kolumn, lub pojedyncza wartość
- width - szerokość kolumn (opcjonalne)
import numpy as npx
import matplotlib.pyplot as plt
# Make a fake dataset:
height = [3, 12, 5, 18, 45]
bars = ('A', 'B', 'C', 'D', 'E')
y_pos = np.arange(len(bars))
# Create bars
plt.bar(y_pos, height)
# Create names on the x-axis
plt.xticks(y_pos, bars)
# Show graphic
plt.show()
By wygenerować wykres kolumnowy poziomy należy użyć metody
plt.barh(y, height)
# libraries
import numpy as np
import matplotlib.pyplot as plt
# Make fake dataset
height = [3, 12, 5, 18, 45]
bars = ('A', 'B', 'C', 'D', 'E')
y_pos = np.arange(len(bars))
# Create horizontal bars
plt.barh(y_pos, height)
# Create names on the y-axis
plt.yticks(y_pos, bars)
# Show graphic
plt.show()
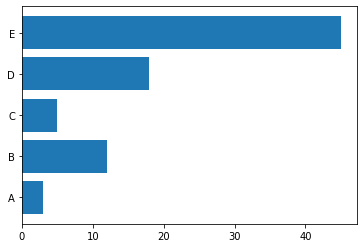
puchar_domow = {
"Slytherin": {
"Obrona przed Czarną Magią": 100,
"Eliksiry" : 200,
"Transmutacja": 150,
"Zielarstwo": 50
},
"Gryffindor":{
"Obrona przed Czarną Magią": 120,
"Eliksiry" : 180,
"Transmutacja": 300,
"Zielarstwo": 120
},
"Ravenclaw":
{
"Obrona przed Czarną Magią": 140,
"Eliksiry" : 120,
"Transmutacja": 130,
"Zielarstwo": 150
},
"Hufflepuff":
{
"Obrona przed Czarną Magią": 120,
"Eliksiry" : 120,
"Transmutacja": 120,
"Zielarstwo": 120
}
}
import matplotlib.pyplot as plt
import numpy as np
barWidth = 0.3
for index, dom in enumerate(puchar_domow):
plt.bar(
3*np.arange(len(list(puchar_domow[dom].keys())))+(index*barWidth), #musimy przesunąć kolumny tak by na siebie nie nachodziły
list(puchar_domow[dom].values()),
width = barWidth,
label=str(dom))
plt.xticks([0.5, 3.5, 6.5, 9.5], list(puchar_domow['Slytherin'].keys()))
plt.legend()
plt.show()
import matplotlib.pyplot as plt
import numpy as np
barWidth = 0.3
temp = []
temp.append(np.zeros(4))
for index, dom in enumerate(puchar_domow):
if index == 0:
continue
temp.append(list(puchar_domow[list(puchar_domow.keys())[index-1]].values()))
sum_temp = np.zeros(4)
for index, dom in enumerate(puchar_domow):
sum_temp += temp[index]
plt.bar(
list(puchar_domow[dom].keys()),
list(puchar_domow[dom].values()),
width = barWidth,
label=str(dom),
bottom=sum_temp) #musimy podać co będzie dołem kolejnych kolumn, żeby je skleić
plt.legend()
plt.show()
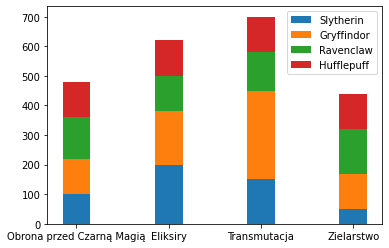
Bardzo popularnym wykresem kolumnowym jest histogram. Histogram to nic innego jak wizualizacja rozkładu jakiejś cechy.
plt.hist(x, bins=None)
Gdzie:
- x - lista danych na podstawie, której chcemy wygenerować histogram
- bins - na ile kolumn chcemy podzielić nasz histogram, domyślnie równa się liczbie unikatowych danych podanych w x. Może być liczbą, albo sekwencją liczb od których uwzględniamy kolejne kolumny
Wygenerujmy dane z rozkładu normalnego i wykreślmy ich histogram.
Źródło: https://matplotlib.org/3.1.1/gallery/pyplots/pyplot_text.html#sphx-glr-gallery-pyplots-pyplot-text-py
import numpy as np
import matplotlib.pyplot as plt
# Fixing random state for reproducibility
np.random.seed(19680801)
mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)
# the histogram of the data
n, bins, patches = plt.hist(x, 50, facecolor='g', alpha=0.75)
plt.xlabel('Smarts')
plt.ylabel('Population')
plt.title('Histogram of IQ')
plt.text(60, 602.5, r'$\mu=100,\ \sigma=15$')
plt.grid(True)
plt.show()
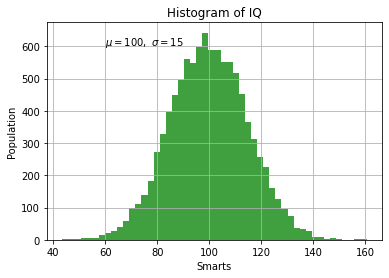
Jeżeli zamiast liczby w populacji interesuje nas prawdopodobieństwo wystąpienia danej kolumny histogramu w metodzie ustawiamy pole density=True.
import numpy as np
import matplotlib.pyplot as plt
# Fixing random state for reproducibility
np.random.seed(19680801)
mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)
# the histogram of the data
n, bins, patches = plt.hist(x, 50, density=True, facecolor='g', alpha=0.75)
plt.xlabel('Smarts')
plt.ylabel('Probability')
plt.title('Histogram of IQ')
plt.text(60, .025, r'$\mu=100,\ \sigma=15$')
plt.xlim(40, 160)
plt.ylim(0, 0.03)
plt.grid(True)
plt.show()
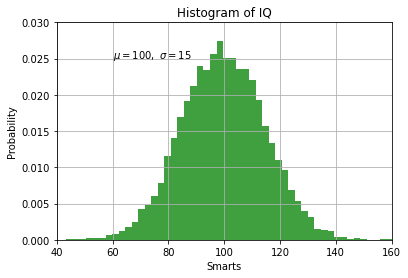
Do generowania histogramu dwuwymiarowego stosujemy polecenie
plt.hist2d(x, y, bins=10, density=False)
Gdzie:
- x, y - wartości na osiach X,Y
- bins - analogicznie do histogramu jednowymiarowego
- density - analogicznie do histogramu jednowymiarowego
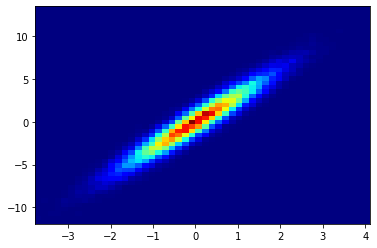
Utworzony wykres jest heat mapą danych
import matplotlib.pyplot as plt
import numpy as np
# create data
x = np.random.normal(size=50000)
y = x * 3 + np.random.normal(size=50000)
# Big bins
plt.hist2d(x, y, bins=(50, 50), cmap=plt.cm.jet)
plt.show()
6. Piecharts - wykresy kołowe
Dotarliśmy do ostatniego kręgu piekła jeżeli chodzi o wizualizację danych. Wykresy kołowe owiane złą sławą są z reguły niepotrzebne, a nasze dane możemy przedstawić w innej, lepszej formie. Jeżeli jednak uprzemy się na nie, je również można zrealizować w matplotlib.
import matplotlib.pyplot as plt
tasks = 'task_1', 'task_2', 'task_3', 'task_4', \
'task_5', 'task_6', 'task_7', 'task_8', \
'task_9', 'task_10', 'task_11', 'task_12', \
'task_13', 'task_14', 'task_15', 'task_16', \
'task_17', 'task_18', 'task_19'
time =[0.722539930138737,
0.28336817817762494 + 0.5273803339805454,
0.1135483211837709 + 0.13343579485081136,
0.8881094930693507 + 0.3978329210076481 + 0.34098400291986763 + 0.4007001109421253 + 0.3937181669753045,
3.1206228479277343 + 4.390893992036581 + 4.731932940194383 + 3.0876565920189023 + 15.17197903408669,
0.052445481065660715 + 0.019446991849690676 + 0.019331110874190927 + 0.09747512708418071 + 0.060720112873241305,
0.029143241932615638,
0.7307675471529365,
0.10479382984340191,
0.4169424350839108,
1.1366547809448093,
1.5477838290389627,
0.05833269190043211,
0.12475891201756895,
0.08382681896910071,
0.0744338259100914,
0.0875642818864435,
0.11377762793563306,
0.04675672412849963]
colors = ['red',
'pink',
'orange',
'purple',
'indigo',
'blue',
'lightblue',
'cyan',
'teal',
'green',
'lightgreen',
'yellowgreen',
'yellow',
'gold',
'orange',
'darkorange',
'brown',
'gray',
'darkslategray']
plt.figure(figsize=(15, 10))
patches = plt.pie(time,
colors=colors,
radius=1,
)
plt.legend(tasks, bbox_to_anchor=(1,1),
fontsize=18)
plt.tight_layout()
plt.title("Czas trwania zadania")
plt.show()
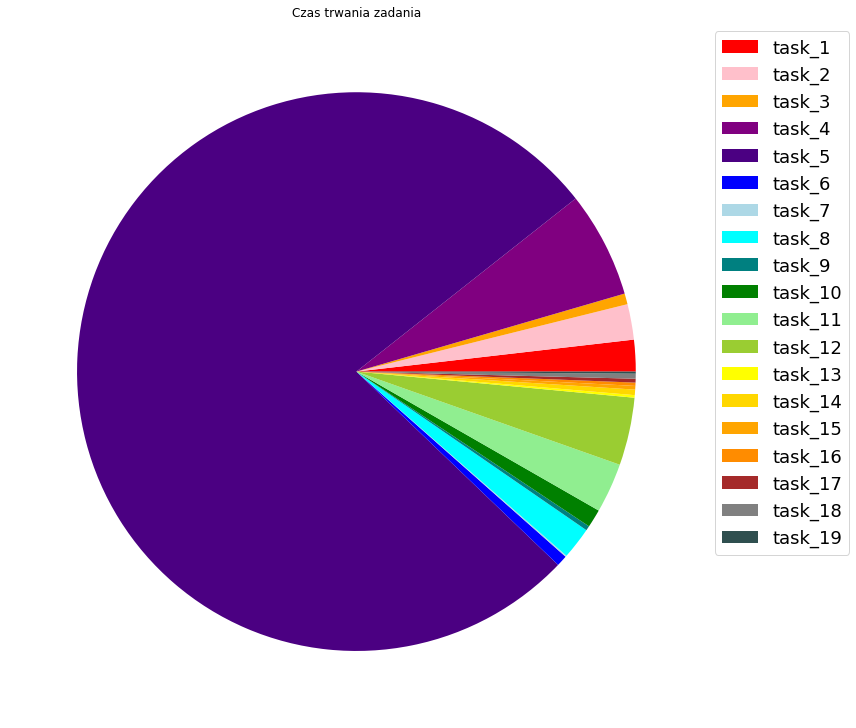
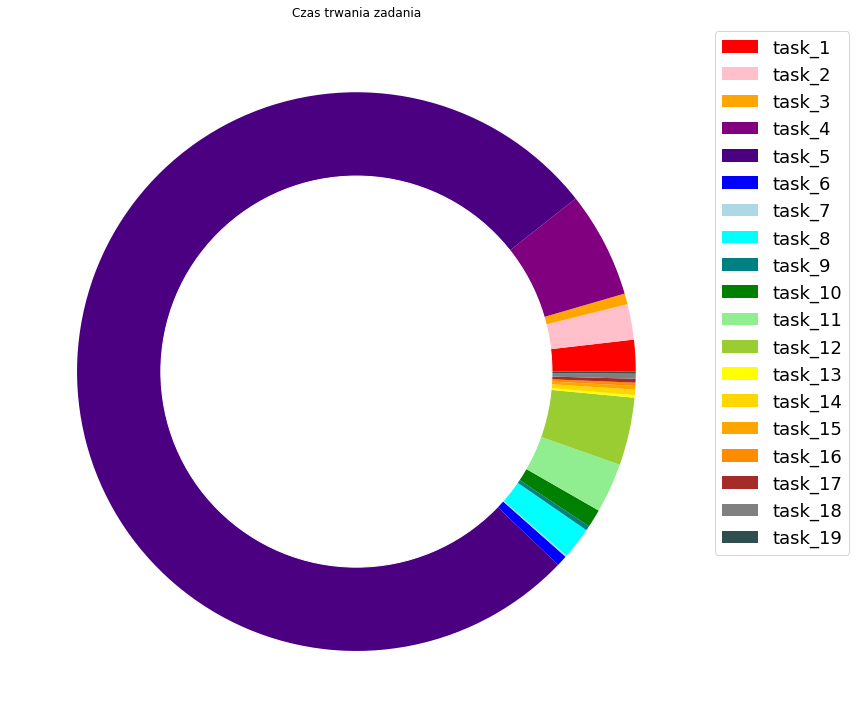
Jedyną informację jaką jesteśmy w stanie wyciągnąć z naszego wykresu jest to, że istnieje jedno zadanie, którego czas trwania stanowi ok. 75% całego czasu. Z wykresu nie jesteśmy w stanie jednak wyczytać ile trwa poszczególne zadanie (możemy dodać tę informację, ale przy dużej liczbie małych fragmentów, będzie to nieczytelne). Dlatego tego typu wykresy mają tylko sens, przy małej liczbie unikatowych kategorii, na które chcemy dzielić nasze dane przy ich wizualizacji.
By poczytać więcej na ten temat zachęcam do lektury:
https://www.businessinsider.com/pie-charts-are-the-worst-2013-6?IR=T
Popularną alternatywą dla wykresu kołowego jest wykres kołowy z wcięciem w środku, tzw. pączek. By go zrobić należy do wykresu dodać białe koło i upozycjonować je na środku wykresu kołowego.
import matplotlib.pyplot as plt
tasks = 'task_1', 'task_2', 'task_3', 'task_4', \
'task_5', 'task_6', 'task_7', 'task_8', \
'task_9', 'task_10', 'task_11', 'task_12', \
'task_13', 'task_14', 'task_15', 'task_16', \
'task_17', 'task_18', 'task_19'
time =[0.722539930138737,
0.28336817817762494 + 0.5273803339805454,
0.1135483211837709 + 0.13343579485081136,
0.8881094930693507 + 0.3978329210076481 + 0.34098400291986763 + 0.4007001109421253 + 0.3937181669753045,
3.1206228479277343 + 4.390893992036581 + 4.731932940194383 + 3.0876565920189023 + 15.17197903408669,
0.052445481065660715 + 0.019446991849690676 + 0.019331110874190927 + 0.09747512708418071 + 0.060720112873241305,
0.029143241932615638,
0.7307675471529365,
0.10479382984340191,
0.4169424350839108,
1.1366547809448093,
1.5477838290389627,
0.05833269190043211,
0.12475891201756895,
0.08382681896910071,
0.0744338259100914,
0.0875642818864435,
0.11377762793563306,
0.04675672412849963]
colors = ['red',
'pink',
'orange',
'purple',
'indigo',
'blue',
'lightblue',
'cyan',
'teal',
'green',
'lightgreen',
'yellowgreen',
'yellow',
'gold',
'orange',
'darkorange',
'brown',
'gray',
'darkslategray']
plt.figure(figsize=(15, 10))
patches = plt.pie(time,
colors=colors,
radius=1,
)
plt.legend(tasks, bbox_to_anchor=(1,1),
fontsize=18)
plt.tight_layout()
plt.title("Czas trwania zadania")
# dodaj koło na środku
my_circle=plt.Circle( (0,0), 0.7, color='white')
p=plt.gcf()
p.gca().add_artist(my_circle)
plt.show()
import matplotlib.pyplot as plt
tasks = 'task_1', 'task_2', 'task_3', 'task_4', \
'task_5', 'task_6', 'task_7', 'task_8', \
'task_9', 'task_10', 'task_11', 'task_12', \
'task_13', 'task_14', 'task_15', 'task_16', \
'task_17', 'task_18', 'task_19'
time =[0.722539930138737,
0.28336817817762494 + 0.5273803339805454,
0.1135483211837709 + 0.13343579485081136,
0.8881094930693507 + 0.3978329210076481 + 0.34098400291986763 + 0.4007001109421253 + 0.3937181669753045,
3.1206228479277343 + 4.390893992036581 + 4.731932940194383 + 3.0876565920189023 + 15.17197903408669,
0.052445481065660715 + 0.019446991849690676 + 0.019331110874190927 + 0.09747512708418071 + 0.060720112873241305,
0.029143241932615638,
0.7307675471529365,
0.10479382984340191,
0.4169424350839108,
1.1366547809448093,
1.5477838290389627,
0.05833269190043211,
0.12475891201756895,
0.08382681896910071,
0.0744338259100914,
0.0875642818864435,
0.11377762793563306,
0.04675672412849963]
colors = ['red',
'pink',
'orange',
'purple',
'indigo',
'blue',
'lightblue',
'cyan',
'teal',
'green',
'lightgreen',
'yellowgreen',
'yellow',
'gold',
'orange',
'darkorange',
'brown',
'gray',
'darkslategray']
plt.figure(figsize=(15, 10))
plt.bar(tasks, time, color=colors)
plt.tight_layout()
plt.title("Czas trwania zadania")
plt.ylabel("Czas (s)")
plt.show()
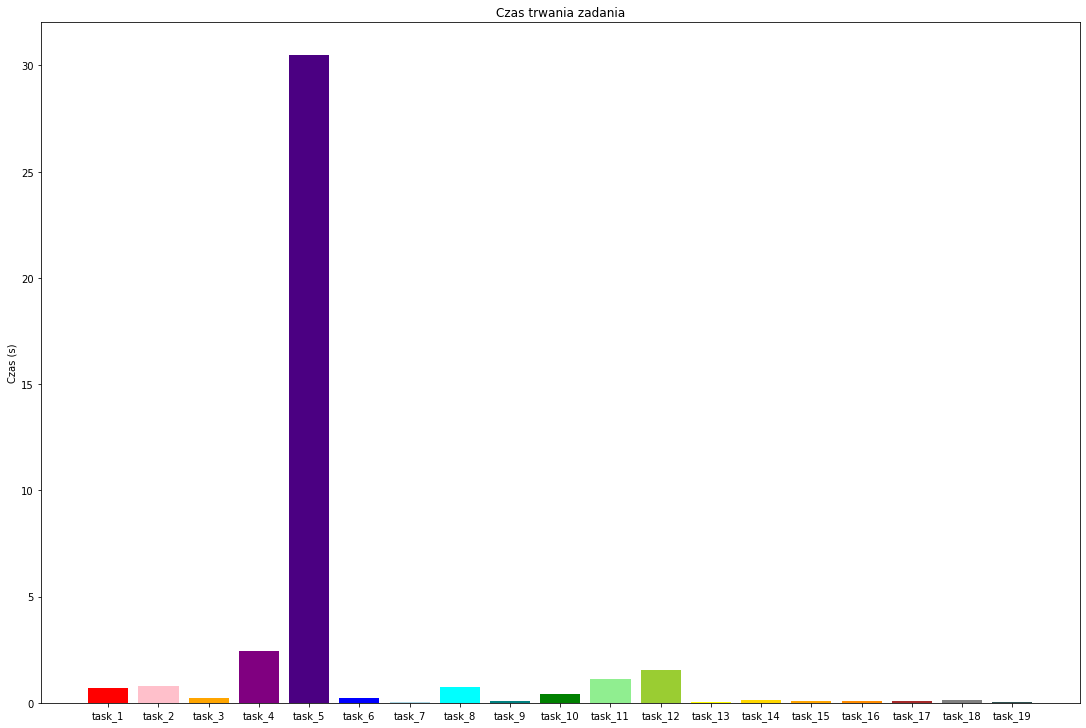
Od razu lepiej. Dla lepszej czytelności możemy zmienić skalę w której wyświetlamy nasze wykresy. Służą do tego polecenia
plt.xscale("skala")
dla osi X
plt.yscale("skala")
dla osi Y
Dopuszczalne wartości:
- ‘linear’ - skala liniowa
- ‘log’ - skala logarytmiczna
- ‘symlog’ - skala logarytmiczna, symetryczna
- ‘logit’ - skala logit
import matplotlib.pyplot as plt
tasks = 'task_1', 'task_2', 'task_3', 'task_4', \
'task_5', 'task_6', 'task_7', 'task_8', \
'task_9', 'task_10', 'task_11', 'task_12', \
'task_13', 'task_14', 'task_15', 'task_16', \
'task_17', 'task_18', 'task_19'
time =[0.722539930138737,
0.28336817817762494 + 0.5273803339805454,
0.1135483211837709 + 0.13343579485081136,
0.8881094930693507 + 0.3978329210076481 + 0.34098400291986763 + 0.4007001109421253 + 0.3937181669753045,
3.1206228479277343 + 4.390893992036581 + 4.731932940194383 + 3.0876565920189023 + 15.17197903408669,
0.052445481065660715 + 0.019446991849690676 + 0.019331110874190927 + 0.09747512708418071 + 0.060720112873241305,
0.029143241932615638,
0.7307675471529365,
0.10479382984340191,
0.4169424350839108,
1.1366547809448093,
1.5477838290389627,
0.05833269190043211,
0.12475891201756895,
0.08382681896910071,
0.0744338259100914,
0.0875642818864435,
0.11377762793563306,
0.04675672412849963]
colors = ['red',
'pink',
'orange',
'purple',
'indigo',
'blue',
'lightblue',
'cyan',
'teal',
'green',
'lightgreen',
'yellowgreen',
'yellow',
'gold',
'orange',
'darkorange',
'brown',
'gray',
'darkslategray']
plt.figure(figsize=(15, 10))
plt.bar(tasks, time, color=colors)
plt.tight_layout()
plt.title("Czas trwania zadania")
plt.ylabel("Czas (s)")
plt.yscale("log")
plt.show()
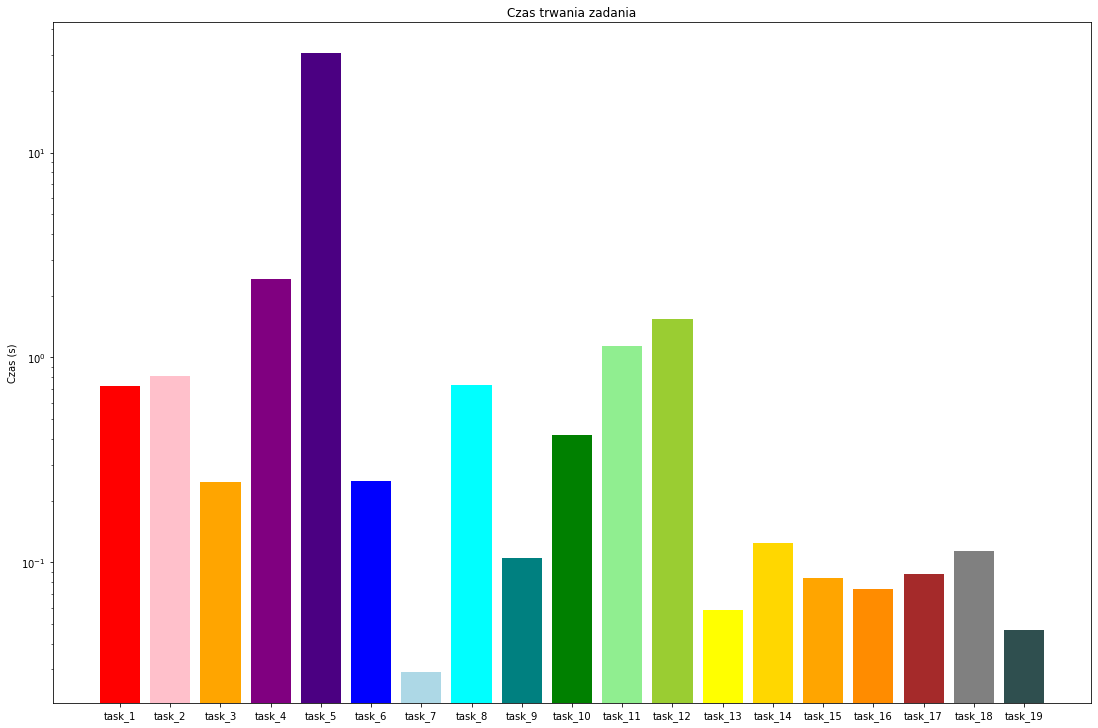
Jak widać mając te same dane, w zależności od tego co chcemy przekazać użyjemy różnych metod do ich wizualizacji. Bardzo ważną częścią pracy z danymi jest umiejętny dobór narzędzi do wizualizacji danych. Ludzie są wzrokowcami, często prawidłowe dane, przedstawione w nieprawidłowy sposób prowadzą do niewłaściwych wniosków.
Polecam poczytać o 5 rzeczach, na które warto zwrócić uwagę analizując wykresy
7. Polar - wykresy liczb urojonych
Do wykresów liczb zespolonych istnieje specjalny wykres zwany polar.
plt.polar(theta, r)
Gdzie:
- theta - lista kątów
- r - lista promieni
W konwencji tej 0 stopni oznacza liczbę rzeczywistą pozytywną, 180 stopni liczbę rzeczywistą negatywną, 90 stopni liczbę urojoną pozytywną, a 270 stopni liczbę urojoną ujemną. Wszystkie pozostałe stopnie to mieszanka liczb urojonych i liczb rzeczywistych czyli liczby zespolone.
Źródło: https://www.geeksforgeeks.org/plotting-polar-curves-in-python/
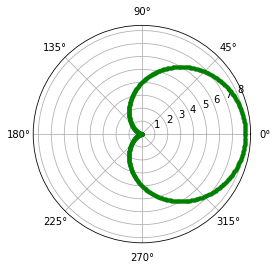
Kardioida (wykres sercowy)
\[r = a + a \cos{\theta}\]import numpy as np
import matplotlib.pyplot as plt
import math
# setting the axes
# projection as polar
plt.axes(projection = 'polar')
# setting the length of
# axis of cardioid
a=4
# creating an array
# containing the radian values
rads = np.arange(0, (2 * np.pi), 0.01)
# plotting the cardioid
for rad in rads:
r = a + (a*np.cos(rad))
plt.polar(rad,r,'g.')
# display the polar plot
plt.show()
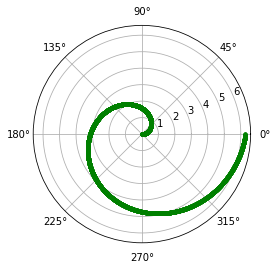
Spirala Archimedesa
\[r = \theta\]import numpy as np
import matplotlib.pyplot as plt
# setting the axes
# projection as polar
plt.axes(projection = 'polar')
# creating an array
# containing the radian values
rads = np.arange(0, 2 * np.pi, 0.001)
# plotting the spiral
for rad in rads:
r = rad
plt.polar(rad, r, 'g.')
# display the polar plot
plt.show()
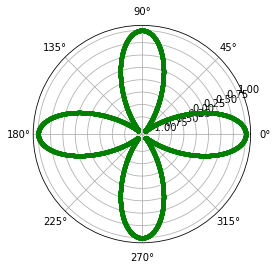
Krzywa róży
\[r = a \cos({n \theta})\]import numpy as np
import matplotlib.pyplot as plt
# setting the axes
# projection as polar
plt.axes(projection='polar')
# setting the length
# and number of petals
a = 1
n = 4
# creating an array
# containing the radian values
rads = np.arange(0, 2 * np.pi, 0.001)
# plotting the rose
for rad in rads:
r = a * np.cos(n*rad)
plt.polar(rad, r, 'g.')
# display the polar plot
plt.show()
8. Obsługa obrazów - PIL
Poza generowaniem własnych wykresów biblioteka matplotlib umożliwia wczytywanie i wyświetlanie obrazów.
Odpowiednio:
plt.imread(fname, format=None)
Gdzie:
- fname - ścieżka do pliku na dysku, sama nazwa pliku jeżeli znajduje się w tym samym folderze co plik pythona, który uruchamiamy
- format - format pliku, jeżeli nie jest sprecyzowany, domyślnie próbuje otworzyć plik w formatowaniu PNG
plt.imshow(X, cmap=None)
Gdzie:
- X - obiekt PIL lub tablica o określonych rozmiarach:
- (M, N)
- (M, N, 3): obraz RGB, wartości rzeczywiste z zakresu 0-1, lub całkowite z zakresu 0-255
- (M, N, 4): jak wyżej, z uwzględnieniem kanału przezroczystości alpha
- cmap - paleta kolorów, dla obrazów czarnobiałym warto zdefiniować odpowiednią paletę kolorów
Matplotlib posiada wiele palet kolorystycznych, poniżej znajduje się ich lista:
https://matplotlib.org/examples/color/colormaps_reference.html
import matplotlib.pyplot as plt
from google.colab import drive #polecenia potrzebne tylko w arkuszu Google by załadować zdjęcia z dysku Google, nie używać u siebie
drive.mount('/content/drive')
filter_img = plt.imread('/content/drive/My Drive/Warsztaty/filter.jpg')
plt.imshow(filter_img)
Mounted at /content/drive
<matplotlib.image.AxesImage at 0x7f6509650630>

PIL (Python Imaging Library)
jest standardową biblioteką do przechowywania obrazów w Pythonie. Biblioteka ta jednak przestała być rozszerzana przez autora w 2011 i nie jest kompatybilna z obecną wersją Pythona. Z tego powodu powstał fork tej biblioteki, który nazywa się Pillow, który jest aktualny z obecną wersją Pythona, a przy okazji w dużej mierze kompatybilny z oryginalnym PILem. Ze względów semantycznych importuje się go jako PIL, mimo iż to co pracuje pod jego kopułą to w rzeczywistości pillow.
import PIL
import matplotlib.pyplot as plt
image = PIL.Image.open('/content/drive/My Drive/Warsztaty/filter.jpg')
plt.imshow(image) #działa tak samo, lecz obiekt PIL posiada o wiele więcej możliwości!
<matplotlib.image.AxesImage at 0x7f6508bc57f0>

Już wcześniej wspomnieliśmy, że numpy jest domyślnym sposobem przechowywania informacji w Pythonie jeżeli chodzi o analizę danych, operację wykonywane na nim są stosunkowo szybkie.
Z tego też powodu istnieje możliwość konwersji obiektów PIL do tablic n-wymiarowych numpy i odwrotnie. Logika jest taka, gdy potrzebujemy wysokiej funkcjonalności na obrazie - operujemy na obiekcie PIL, jeżeli potrzebujemy dokonać obliczeń - dokonujemy ich na macierzy numpy.
Przykładowe konwersje macierzy numpy do obiektu PIL:
PIL_image = Image.fromarray(np.uint8(numpy_image)).convert('RGB')
PIL_image = Image.fromarray(numpy_image.astype('uint8'), 'RGB')
Przykładowe konwersje obiektu PIL do macierzy numpy :
macierz = numpy.asarray(PIL.Image.open('obraz.jpg'))
W obu przypadkach ważne jest kodowanie obiektów, musimy dostosować by kodowanie w jednej wersji było kompatybilne do kodowania w drugiej wersji, najlepiej operować na kodowaniu np.uint8 czyli liczbach całkowitych z zakresu 0-255. Jeżeli jest jakiś problem z obrazem w naszym kodzie zawsze warto jest sprawdzić czy aby na pewno korzystamy z dobrego kodowania.
Macierze numpy są wykorzystywane również przez OpenCV z tego względu, jest to unikatowy sposób zapisu naszych obrazów. Warto opanować tę umiejętność.
Praca domowa
Spróbuj przygotować wybrany przez siebie wykres na podstawie jakichś danych zebranych w zestawieniu, raporcie, etc. Zbiór danych nie powinien być zbyt duży, ponieważ jeszcze nie opanowaliśmy jak pracować na dużych zbiorach. Porównaj przedstawienie tych samych danych na różnych wykresach. Jakie wykresy pasują do wizualizacji danego zagadnienia?
Przykładowe raporty:
- https://www.theesa.com/esa-research/2020-essential-facts-about-the-video-game-industry/
- https://polishgamers.com/
- https://gs.statcounter.com/screen-resolution-stats/mobile/worldwide
- https://stat.gov.pl/podstawowe-dane/
- https://ec.europa.eu/eurostat/web/main/home
Przykładowe kody:
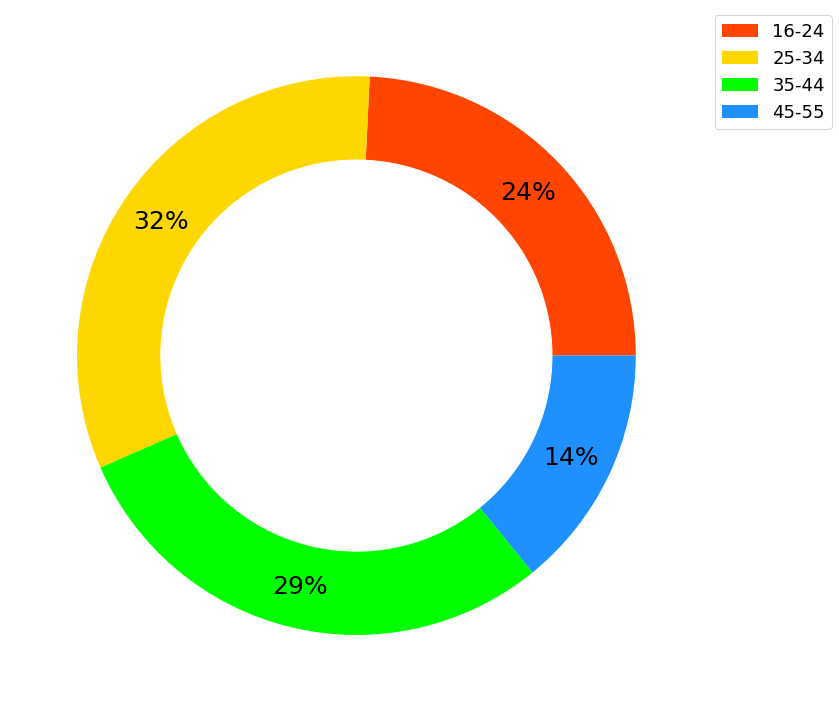
import matplotlib.pyplot as plt
age_group = '16-24', '25-34', '35-44', '45-55'
percentage = [24, 32, 29, 14]
colors = ['orangered',
'gold',
'lime',
'dodgerblue',
]
plt.figure(figsize=(15, 10))
patches = plt.pie(percentage,
colors=colors,
autopct='%1.0f%%',
pctdistance=0.85,
textprops={'fontsize': 25})
plt.legend(age_group, bbox_to_anchor=(1, 1),
fontsize=18)
plt.tight_layout()
# plt.title("Procentowy udział")
# dodaj koło na środku
my_circle = plt.Circle((0, 0), 0.7, color='white')
p = plt.gcf()
p.gca().add_artist(my_circle)
plt.show()
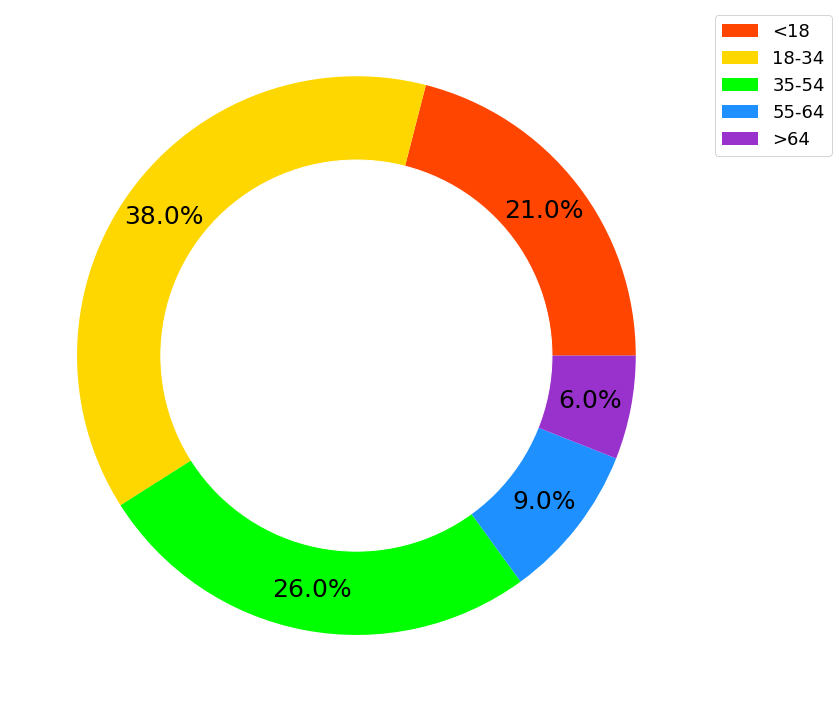
import matplotlib.pyplot as plt
age_group = '<18', '18-34', '35-54', '55-64', '>64'
percentage = [21, 38, 26, 9, 6]
colors = ['orangered',
'gold',
'lime',
'dodgerblue',
'darkorchid'
]
plt.figure(figsize=(15, 10))
patches = plt.pie(percentage,
colors=colors,
autopct='%1.1f%%',
pctdistance=0.85,
textprops={'fontsize': 25})
plt.legend(age_group, bbox_to_anchor=(1, 1),
fontsize=18)
plt.tight_layout()
# plt.title("Procentowy udział")
# dodaj koło na środku
my_circle = plt.Circle((0, 0), 0.7, color='white')
p = plt.gcf()
p.gca().add_artist(my_circle)
plt.show()
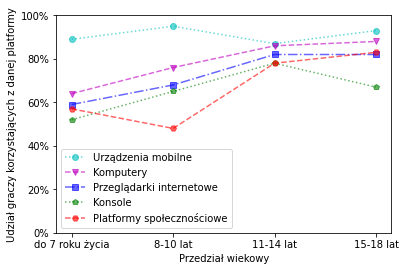
import matplotlib.pyplot as plt
smartphone = [89, 95, 87, 93]
pc = [64, 76, 86, 88]
web = [59, 68, 82, 82]
console = [52, 65, 78, 67]
social = [57, 48, 78, 83]
plt.plot(smartphone, "co:", alpha=0.6, label="Urządzenia mobilne")
plt.plot(pc, "mv--", alpha=0.6, label="Komputery")
plt.plot(web, "bs-.", alpha=0.6, label="Przeglądarki internetowe")
plt.plot(console, "gp:", alpha=0.6, label="Konsole")
plt.plot(social, "rH--", alpha=0.6, label="Platformy społecznościowe")
plt.legend()
plt.xlabel("Przedział wiekowy")
plt.ylim(0,100)
plt.xticks(ticks=[0, 1, 2, 3], labels=["do 7 roku życia", "8-10 lat", "11-14 lat", "15-18 lat"])
plt.ylabel("Udział graczy korzystających z danej platformy")
plt.yticks(ticks=[0,20,40,60,80,100], labels=["0%","20%","40%","60%","80%","100%"])
plt.show()